The paper considers the problem of dynamic longitudinal–transverse bending of an elastic rod with initial curvatures under short-term axial action. The motivation of the research is the current problems related to the analysis of the stability and strength of structural elements under shock loads, applicable, in particular, to the problems of launching aircraft, pile foundations and vehicles. The main attention is paid to two special cases: the effect of a short-term longitudinal impact of constant force and the application of an axial force that increases linearly over time. The problem statement specifically takes into account the fact that the time range of the load application is half the time of wave propagation along the length of the rod, which makes it possible to correctly simulate wave effects. Unlike classical approximate models, in which the propagation of a longitudinal wave is assumed to be instantaneous and the voltage is assumed to be constant along the rod, equations are used in this work taking into account the finite velocity of propagation of longitudinal waves. To numerically study the dynamics of small transverse deviations, eigenfunction decomposition is applied and a system of ordinary differential equations for Fourier amplitudes is solved. The influence of various shapes of the initial bend is analyzed in detail, as well as changes in the maximum oscillation amplitudes for various parameters of the model. A comparative analysis of the behavior of the rod for simple and complex initial forms of curvature is carried out, and the occurrence of irregularities close to those observed in physical experiments is shown. The results obtained confirm the importance of taking into account wave effects in short-term dynamic tasks and expand the scope of the developed models.
elastic rod,
dynamic bending,
short-term impact,
initial curvature,
wave equation,
numerical modeling,
dynamic stability
Dynamic loads, in particular impact, are the most dangerous type of impact on rod systems. It should be noted that during an impact, the speed of movement of the selected element of the rod acquires the final speed in a short period of time. That is, the impact load causes significant accelerations and, accordingly, inertial forces, the direction of action of which is directed in the direction opposite to the acceleration. The complexity of dynamic problems requires the introduction of a number of assumptions:
In the case of dynamic longitudinal action, the modeling task is complicated by the fact that the propagation of longitudinal elastic waves along the rod can cause intense transverse vibrations associated with the initial bending relative to the rectilinear shape of the rod. However, since the propagation time of a longitudinal wave along the length of the rod is significantly less than the smallest period of transverse vibrations, a simplified approximate model is usually used, which assumes that the longitudinal wave propagates along the rod instantly, and the axial compressive force is constant along the length.
In this paper, a hinged pipeline with a given initial curvature and zero initial conditions have been considered. The problem is solved taking into account the finite velocity of wave propagation in the rod for two special cases:
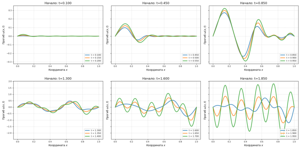
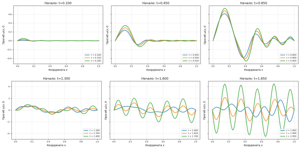
The objectives of this study are to construct models for the presented two subtasks and to numerically investigate the bending of a rod at different initial curvatures.
Methodology. To calculate the rod bending, a dynamic bending equation is used. It is assumed that the longitudinal wave path along the double length of the rod is greater than the impact time.
For the first subtask, a wave equation was additionally used to find the external force
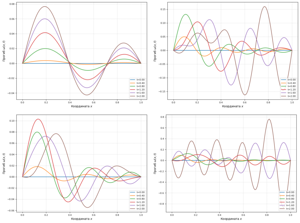
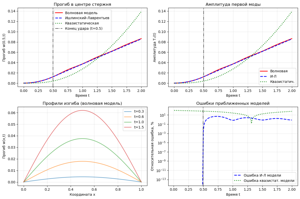
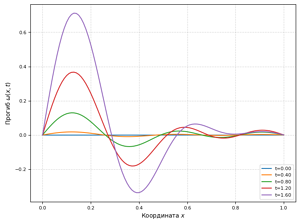
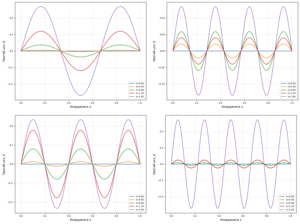
Findings. It is shown that a linearly increasing load at certain specified initial curvatures of a simple shape specifies shapes similar to the Feodosyev model [Feodosyev V.I. Selected Problems and Questions in Strength of Materials. Beekman Books Inc., 1977] and corresponds to a gradual loading of the rod, and if more complex shapes are specified, unevenness begins to appear, as in a physical experiment [Ovchinnikov N.T., Sorokin F.D. Physical modeling and numerical simulation of bar deformation under axial loading in the channel. Part 1. Engineering Journal: Science and Innovation. 2020, in Russian].
The conducted modeling of a short-term impact, taking into account that
Originality. Since, based on the results of the physical experiment, the bend has a slightly different shape due to uncertain parameters, the Feodosyev model is not applicable for precise calculations, as are probably any other static methods. Therefore, it is advisable to develop a combined method for dynamic bending with restrictions when bending in a flat channel, for which variational principles may be useful.