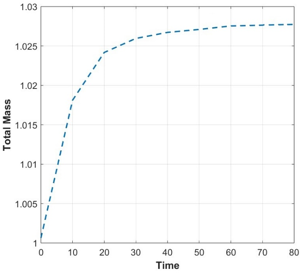
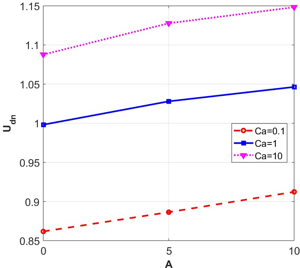
This article examines the influence of a highly viscous region on the deformation of a single droplet moving in a thermoviscous fluid flow with an anomalous viscosity-temperature dependence. Numerical modeling is performed using the phase field method, consisting of the Cahn-Hilliard-Navier-Stokes system of equations, supplemented by an equation for the temperature field. The results of numerical modeling for laminar flow with a steady-state temperature field in a flat channel are presented. The influence of a viscous barrier located in the middle of the channel on the droplet velocity and its deformation is analyzed for three capillary numbers. Graphs of the droplet velocity dependence on the capillary number are plotted. It is shown that for all cases of capillary numbers, the viscous barrier formed in the channel imparts additional acceleration to the droplet. For all calculations, the total normalized mass of the system was calculated over time, and the maximum error is shown to not exceed 5%. The droplet shape at the channel exit is shown for different cases of a viscous barrier. It is shown that if the capillary number is high, inclusions of the surrounding liquid can form in the droplet. However, if the droplet moves through a channel with a viscous barrier, the high-viscosity region prevents the formation of inclusions of other liquids due to more intense droplet deformation. It is established that the relative velocity of a droplet in a flow of an anomalously viscous liquid is higher than in a flow of liquid with a constant minimum viscosity. Graphs of the droplet’s relative velocity versus the liquid anomaly parameter are presented for three capillary numbers. It is shown that the higher the liquid anomaly parameter, the higher the relative velocity of the droplet. It is established that the viscous barrier formed in the channel accelerates the droplet and increases its relative velocity.
phase field model,
Cahn–Hilliard–Navier–Stokes equation,
anomalously viscous liquid,
surface tension,
droplet motion,
laminar flow
In recent years, the study of the properties of anomalously viscous liquids has attracted the interest of many scientists from various fields of science,
from oil refining to medicine. Unlike ordinary liquids, the viscosity of which decreases with increasing temperature, the viscosity of anomalously viscous media changes non-monotonically:
it can increase sharply and then decrease in a certain temperature range. Under certain temperature conditions, an interesting phenomenon occurs in such liquids - a viscous barrier.
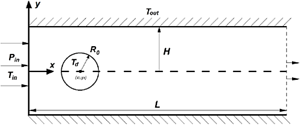
This is a localized region with high viscosity, which can affect the movement of the main liquid flow, up to blockage. In this paper, we study the effect of a viscous barrier on the
velocity of a droplet moving in a flow of an anomalously viscous liquid in a flat channel. Numerical modeling is performed using the phase field method, consisting of a system of
Cahn–Hilliard–Navier–Stokes equations, supplemented by an equation for the temperature field. The purpose of the modeling is to study the effect of a viscous barrier located in the center of
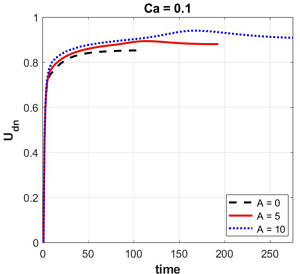
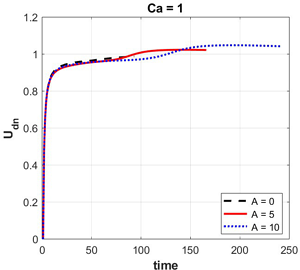
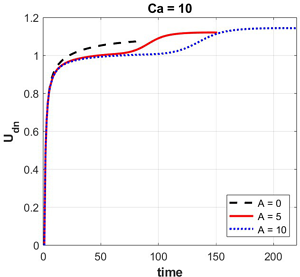
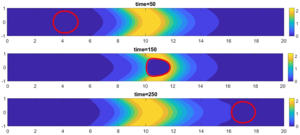
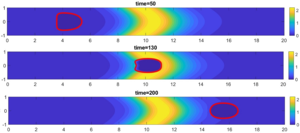
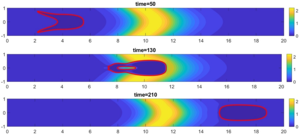
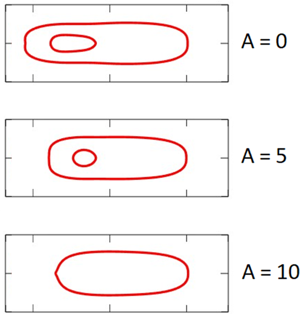
the channel on the velocity and deformation of a droplet. Three values of the capillary number Ca = 0.1, Ca = 1, Ca = 10 and three parameters of the viscosity anomaly
Graphs of the droplet velocity dependence on the capillary number are compiled. It is shown that for all cases of capillary numbers, the viscous barrier formed in the channel imparts additional acceleration to the droplet. For all calculations, the total normalized mass of the system was calculated over time, it is shown that the maximum error does not exceed 5%. Images of the droplet shape at the channel outlet for different cases of a viscous barrier are given. It is shown that if the capillary number is large (Ca > 1), then inclusions of the surrounding liquid can form in the droplet, however, if the droplet moves in a channel with a viscous barrier, then the highly viscous region does not allow inclusions of another liquid to form in the droplet due to more intense deformation of the droplet. It is established that the relative velocity of a drop in a flow of an abnormally viscous liquid is higher than in a flow of liquid with a constant minimum viscosity. Graphs of the dependence of the relative velocity of a drop on the liquid anomaly parameter for three capillary numbers are presented. It is shown that in a channel without a viscous barrier, the relative velocity of a drop is the lowest for all capillary numbers. In a channel with the largest viscous barrier (A = 10), the relative velocity of a drop is the highest. It is evident that the larger the viscous barrier, the stronger the acceleration it imparts to a drop: a viscous barrier acts as a kind of ”viscous gun“, imparting acceleration to a drop and increasing its velocity. It is established that a viscous barrier formed in a channel imparts acceleration to a drop and increases the relative velocity of a drop.