Nasibullaeva E.Sh. Numerical analysis of wave scattering by a pair of soundproof spheres by
orthogonal central compositional design method. Multiphase Systems. 2025;20(3):116–128 (in Russian).
Numerical analysis of wave scattering by a pair of soundproof spheres by orthogonal central compositional design method
Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia
Abstract
In the paper, the analysis of wave scattering on a system of two soundproof spheres was carried out using the orthogonal central compositional
design method. The main objectives of the work are to determine the main parameters, the change of which significantly affects on the
whole system; to determine the variable parameter values of the system, at which the loss functions (the total scattering cross section and
the normalized pressure at a fixed point) take the minimum and maximum values, and to study the system at optimal parameter values. The
orthogonal compositional design method is implemented for a three-factor computational experiment, where three main parameters of
the system were selected as factors: the wave radius, the ratio of the sphere radii, and the distance between the sphere centers. For the
obtained regression equation, the significance of the coefficients was checked using Student’s t-test and the adequacy of the model using
Fisher’s F-test. It was found that in the case of a spherical wave from a monopole radiation source, the nonlinear influence of the factors is
more pronounced than in the case of a plane wave; normal pressure calculated at a fixed point is insensitive to changes in parameters in
the case of a plane wave, as well as in the case of a monopole radiation source for small values of the sphere surface complex conductivity;
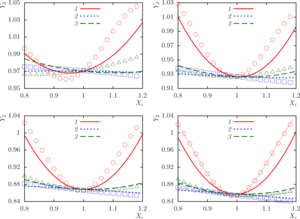
the total scattering cross section is highly sensitive in the case of a system with ideally rigid spheres; the highest and lowest values of the
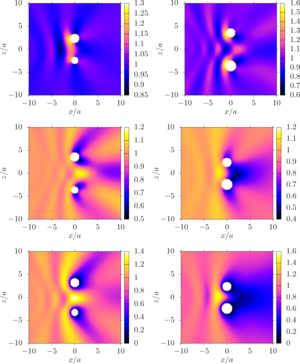
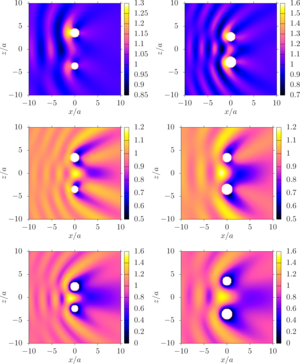
loss functions are achieved at the boundary of the three-dimensional parametric region of factors changes. Pressure distribution diagrams
were constructed, which made it possible to determine the zones of high or low pressure for the found optimal values of the factors.
Keywordsacoustic scattering,
soundproof sphere,
computational experiment,
orthogonal central compositional design method,
total
scattering cross section,
plane wave,
monopole radiation source
Article outline
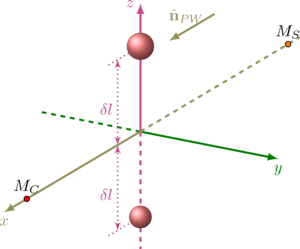
When studying the problem of acoustic wave scattering on a set of small obstacles, the wave scattering on a system consisting of two spheres is of particular interest. This is due to the following. On the one hand, in such systems there is an interaction of fields scattered from spherical particles. On the other hand, this interaction is simple enough to be studied in detail. In this paper, for the first time, an analysis of the scattering of a wave (plane wave or spherical wave from a monopole radiation source) on a system of two soundproof (the wave does not pass through the surface) spheres is carried out using the orthogonal central compositional design method. This method is implemented for a three-factor computational experiment, where one physical (wave radius) and two geometric (the ratio of the radii of the spheres and the characteristic distance between the centers of the spheres) parameters of the system are taken as factors.
The main purpose of the work are to determine the main parameters (factors), the change of which significantly affects on the whole system; to determine the values of the system variable parameters, at which the loss functions (the total scattering cross-section and the normalized pressure at a fixed point) take the minimum and maximum values, as well as to study the system at optimal values of the parameters.
Methodology. Since it is necessary to vary several parameters of the system when conducting a series of computational experiments, the orthogonal central compositional design method based on regression analysis methods was used to take into account the quadratic contributions of factors. For the obtained regression equation, the significance of the coefficients was checked using Student's t-test and the adequacy of the model using Fisher's F-test. The minimum and maximum values of the loss functions were determined using analytical methods of the theory of several variable functions.
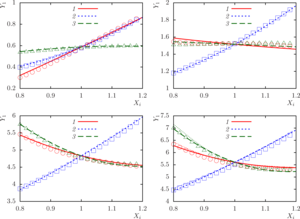
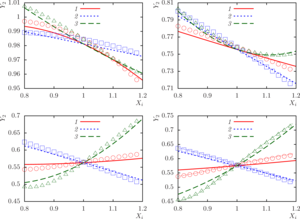
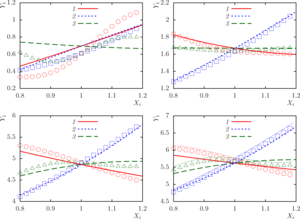
Findings. As a result of applying the presented numerical method, the following results were obtained:
- in the case of a spherical wave from a monopole radiation source, the nonlinear influence of factors is more pronounced than in the case of a plane wave;
- the loss function characterizing the normal pressure at a point is insensitive to changes in parameters in the case of a plane wave, as well as in the case of a monopole radiation source for small values of complex total admittance;
- the loss function characterizing the total scattering cross section is very sensitive in the case of a system with perfectly rigid spheres;
- in almost all cases, the highest and lowest values of the objective functions are achieved at the boundary of the three-dimensional parametric region of factors change.
The pressure distribution diagrams constructed for the found optimal values of the factors made it possible to identify zones of high or low pressure. Behind the system of two spheres, zones similar to the case of a single sphere were discovered, where the pressure is close in value to the pressure of the incident wave (the so-called Poisson spot, namely, there is a brightening of the shadow zone behind the sphere). For a system of a pair of spheres, such zones are observed both in the case of a plane wave and for a spherical wave from a monopole radiation source.
Value. In the future, it is planned to conduct research for the case of sound-permeable spheres. The results obtained in this work showed that the value of the complex total admittance greatly changes the overall picture. The difference is especially strong in the limiting cases of ideally rigid and soft spheres, to which the cases of sound-permeable spheres are close, namely, liquid drops in gas and gas bubbles in liquid (outside the resonance region).
References
- Embleton TFW. Mutual Interaction between Two Spheres in a Plane Sound Field. J. Acoust. Soc. Am. 1962;34(11):1714–1720.
DOI: 10.1121/1.1909104
- Марневская ЛА. К дифракции плоской скалярной волны на двух сферах. Акустический журнал. 1968;14(3):427–434.
Marnevskaya LA. On diffraction of a plane scalar wave on two spheres. Akusticheskij Zhurnal. 1968;14(3):427–434 (in Russian).
http://www.akzh.ru/pdf/1968_3_427-434.pdf
- Марневская ЛА. О рассеянии плоской волны на двух акустически жестких сферах. Акустический журнал. 1969;15(4):579–583.
Marnevskaya LA. To scattering of a plane wave on two acoustic rigid spheres. Akusticheskij Zhurnal. 1969;15(4):579–583 (in Russian).
http://www.akzh.ru/pdf/1969_4_579-583.pdf
- Bruning JH, Lo YT. Multiple scattering by spheres. UIUC EM Lab Technical Report, Illinois; 1969. 169 p.
https://wcchew.ece.illinois.edu/chew/Efficient_Addition_Theorem/BL_MSUR.pdf
- New R, Eisler TJ. Acoustic radiation from multiple spheres. Journal of Sound and Vibration. 1972;22(1):1–17.
DOI: 10.1016/0022-460x(72)90839-5
- Peterson B, Str"om S. Matrix formulation of acoustic scattering from an arbitrary number of scatterers. J. Acoust. Soc. Am. 1974;56(3):771–780.
DOI: 10.1121/1.1903325
- Gaunaurd GC, Huang H, Strifors H. Acoustic scattering by a pair spheres. J. Acoust. Soc. Am. 1995;98(1):495–507.
DOI: 10.1121/1.414447
- Лебедев АВ, Хилько АИ. Интегральный поперечник рассеяния плоской акустической волны на двух близко расположенных импедансных сферах. Акустический журнал. 1997;43(5):661–667.
Lebedev AV, Hil'ko AI. The Integral Scattering Cross-Section of a Plane Acoustic Wave from Two Dose Impedance Spheres. Akusticheskij Zhurnal. 1997;43(5):661–667 (in Russian).
http://www.akzh.ru/pdf/1997_5_661-667.pdf
- Gabrielli P, Mercier-Finidori M. Acoustic Scattering By Two Spheres: Multiple Scattering And Symmetry Considerations. Journal of Sound and Vibration. 2001;241(3):423–439.
DOI: 10.1006/Jsvi.2000.3309
- Шарфарец БП. Метод решения задач множественного рассеяния на нескольких телах в однородной безграничной среде. Акустический журнал. 2005;51(5):672–681.
EDN: HRYEMF
Sharfarets BP. Method for solving the problems of multiple scattering by several bodies in a homogeneous unbounded medium. Acoustical Physics. 2005;51(5):578–586.
DOI: 10.1134/1.2042578
- Румелиотис ДА, Котсис АД. Рассеяние звуковых волн на двух сферических телах, одно из которых имеет малый радиус. Акустический журнал. 2007;53(1):38–49.
EDN: HYPTWR
Roumeliotis JA, Kotsis AD. Acoustic scattering from two spheres, one with a small radius. Acoustical Physics. 2007;53(1):33–43.
DOI: 10.1134/S1063771007010046
- Насибуллаева ЭШ. Исследование акустического рассеяния от пары звуконепроницаемых сфер при внешнем воздействии.Многофазные системы. 2019;14(1):44–51.
Nasibullaeva ESh. Investigation of acoustic scattering from a pair soundproof spheres under external influence. Multiphase Systems. 2019;14(1):44–51 (in Russian).
DOI: 10.21662/mfs2019.1.006
- Насибуллаева ЭШ. Рассеяние звуковых волн на сферах: методы решения и основные характеристики (обзор). Многофазные системы. 2021;16(3–4):88–104.
Nasibullaeva ESh. Scattering of sound waves on spheres: methods and main characteristics (review). Multiphase Systems. 2021;16(3–4):88–104 (in Russian).
DOI: 10.21662/mfs2021.3.013
- Володарский ЕТ, Малиновский БН, Туз ЮМ. Планирование и организация измерительного эксперимента. Киев: Высшая школа; 1987. 280 c.
Volodarsky ET, Malinovsky BN, Tuz YuM. Designing and Organizing of a Measurement Experiment. Kiev: Vysshaya shkola; 1987. 280 p. (in Russian).
- Петков АА. Ортогональное центральное композиционное планирование в технике и электрофизике высоких напряжений: учеб.-метод. пособие. Харьков: НТУ «ХПИ»; 2007. 61 с.
Petkov AA. Orthogonal Central Compositional Designing in Technology and High Voltage Electrophysics: Educational and Methodological Manual. Kharkov: NTU «KhPI»; 2007. 61 p. (in Russian).
- Реброва ИА. Планирование эксперимента: учеб. пособие. Омск: СибАДИ; 2010. 105 с.
Rebrova IA. Designing an Experiment: Tutorial. Omsk: SibADI; 2010. 105 p. (in Russian).
- Казаков АВ. Планирование эксперимента и измерение физических величин: учеб. пособие. Пермь: Изд-во Перм. нац. иссслед. политехн. ун-та; 2014. 89 с.
Kazakov A.V. Designing an Experiment and Measuring Physical Quantities: Tutorial. Perm: Izdatel'stvo Permskogo natsional'nogo isssledel'skogo politekhnicheskogo universiteta; 2014. 89 p. (in Russian).
- Oyejola BA, Nwanya JC. Selecting the Right Central Composite Design. International Journal of Statistics and Applications. 2015;5(1):21–30.
http://article.sapub.org/10.5923.j.statistics.20150501.04.html
- Владимиров ВС. Уравнения математической физики. Москва: Наука; 1981. 512 с.
Vladimirov VS. Equations of Mathematical Physics. New York: Marcell Dekker Incoporated; 1971. 427 p.
- Gumerov NA, Duraiswam iR. Computation of scattering from N spheres using multipole reexpansion. J. Acoust. Soc. Am. 2002;112(6):2688–2701.
DOI: 10.1121/1.1517253
- Корн Г, Корн Т. Справочник по математике для научных работников и инженеров. Москва: Наука; 1974. 832 с.
Korn GA, Korn ThM. Mathematical Handbook for Scientists and Engineers. New York: McGraw Hill Book Company; 1968. 943 p.
- Насибуллаева ЭШ. Моделирование акустического рассеяния от множества звукопроницаемых сфер в трехмерном пространстве. Вычислительные технологии. 2022;27(2):19–36.
Nasibullaeva ESh. Simulation of Acoustic Scattering from a Set of Sound-permeable Spheres in 3D Space. Computational Technologies. 2022;27(2):19–36. (in Russian).
DOI: 10.25743/ICT.2022.27.2.003
- Насибуллаева ЭШ. Численный анализ многократного рассеяния акустической волны на множестве звукопроницаемых сфер в трехмерном пространстве. Вычислительная механика сплошных сред. 2022;15(4):383–398.
Nasibullaeva ESh. Numerical Analysis of Multiple Scattering of an Acoustic Wave on a Set of Sound-permeable Spheres in 3D Space. Computational Continuum Mechanics. 2022;15(4):383–398 (in Russian).
DOI: 10.7242/1999-6691/2022.15.4.29
- Иванов ЕА. Дифракция электромагнитных волн на двух телах. Минск: Наука и техника; 1968. 584 с.
Ivanov YeF. Diffraction of electromagnetic waves on two bodies. Washington: National Aeronautics and Space Administration; 1970. 597 p.
- Насибуллаев ИШ. Использование свободных программ для обработки и визуализации результатов научных исследований. Многофазные системы. 2021;16(2):58–71.
Nasibullayev ISh. Application of Free Software for Processing and Visualization of Scientific Research Results. Multiphase Systems. 2021;16(2):58–71 (in Russian).
DOI: 10.21662/mfs2021.2.009
- Блохин АВ. Теория эксперимента. Курс лекций. В 2х частях. Часть 2. Минск: Белорусский государственный университет; 2002. 67 с.
Blokhin AV. Theory of experiment. Lecture course. In 2 parts. Part 2. Minsk: Belarusian State University; 2002. 67 p. (in Russian)
- Доерфель К. Статистика в аналитической химии. Москва: Мир; 1969. 247 с.
Doerffel K. Statistik in der analytischen Chemie. Leipzig: Deutscher Verlag f"ur Grundstoffindustrie; 1966. 211 p. (in Deutsch)
- Адлер ЮП, Маркова ЕВ, Грановский ЮВ. Планирование эксперимента при поиске оптимальных условий. Москва: Наука; 1976. 254 с.
Adler UP, Markova EV, Granovskiy UV. Experiment disign with selecting the optimal conditions. Moscow: Nauka; 1976. 280 p. (in Russian)
- Duda RO, Martens WL. Range dependence of the response of a spherical head model.
J. Acoust. Soc. Am. 1998;104(5):3048–3058.
DOI: 10.1121/1.423886
- Гринченко ВТ, Вовк ИВ, Мацыпура ВТ. Основы акустики. Киев: Наукова думка; 2009. 867 с.
Grinchenko VT, Vovk IV, Macypura VT. Basics of acoustics.
Kiev: Naukova Dumka; 2009. 867 p. (in Russian).