ISSN 2658–5782
DOI 10.21662
DOI 10.21662
Electronic Scientific Journal
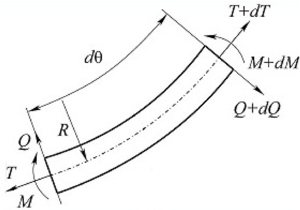
An analytical geometrically nonlinear model of flexible single-layer graphene or a flexible beam is presented, for an element of which the equilibrium equations are written in projections of forces onto natural coordinate axes: tangent, normal to the axis, and the sum of moments relative to the axis coinciding with the binormal. The bending moment is defined as the product of the bending rigidity and the change in curvature taken in exact form. 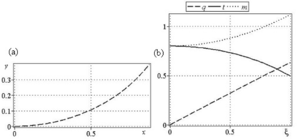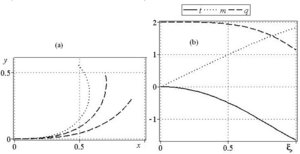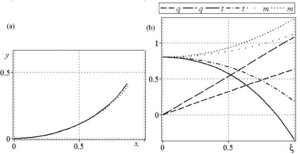A nonlinear boundary value problem for single-layer graphene or a flexible beam in a deformed state is formulated in dimensionless form and exact analytical general solutions are obtained in elliptic functions, based on which the deformation modes of the flexible beam, distribution of tension forces, shear forces, and bending moments are determined. An exact analytical solution is also given for the case of a dimensionless bending moment acting at the free end with zero shear force in elliptic functions. The action of the tension force is taken into account by a parameter depending on the curvature and the tension force at the free end. Formulas for finding the shape of single-layer graphene or a flexible beam and dimensionless tension forces are obtained. The shear force and bending moment are calculated accordingly. If the tension force at the free end is zero, the curvature of the cross-section is also zero, so the bending moment is zero, then the differential equation of bending is simplified. Taking into account the effect of the average pressure does not complicate the task. In the differential equation, an additional parameter appears for the desired function, taking into account the effect of the average pressure. The effect of the average pressure depends on the thickness of the flexible single-layer graphene or flexible beam.
single-layer graphene,
cylindrical bending,
shape,
forces,
shear forces,
bending moment
Linear bending of a cantilever rod under all-round pressure and longitudinal force is considered by M.A. Ilgamov in static and dynamic settings. The transverse distributed force on the rod is taken into account, arising during bending as a result of the formation of a difference in the areas of the convex and concave parts of the surface. As noted in the work of M.A. Ilgamov, starting with the generalizing works on the theory of thin plates and shells Rayleigh, Love the transverse distributed force is taken to be equal to the pressure difference. Taking into account the difference in the areas of the convex and concave surfaces, appearing during bending of the rod and cylindrical bending of the plate, leads to a distributed transverse force directed towards the concavity.
B.D. Annin and co-authors present an analytical geometrically nonlinear model of a flexible cylindrical frame (rim) of a transformable precision large-sized reflector of antennas used in space technology, manufactured using polymer composite materials with shape memory. Using a geometrically nonlinear model, accurate analytical solutions are obtained that allow one to determine preliminary geometric dimensions and optimal shape of the flexible frame, as well as to estimate the accumulated energy.
Here, an analytical geometrically nonlinear model of flexible single-layer graphene or a flexible beam is presented, taking into account the effect of average pressure. The problem of determining the shape, forces and moments in single-layer graphene is set. For an element of single-layer graphene or a flexible beam, equilibrium equations are written in projections of forces on natural coordinate axes: tangent, normal to the axis and the sum of moments relative to the axis coinciding with the binormal. The bending moment is defined as the product of the bending rigidity and the change in curvature, taken in exact form. It is found that the general solution of the differential equation is expressed through elliptic functions. It is found that with an increase in the shear force, the deflections of single-layer graphene increase. Taking into account the effect of the average pressure does not complicate the problem. In the differential equation, an additional parameter appears at the desired function, taking into account the effect of the average pressure. The effect of the average pressure depends on the thickness of the flexible single-layer graphene or flexible beam. The results of the work can be used in the calculation of thin-walled structural elements such as shells, plates, under the action of high pressures.
