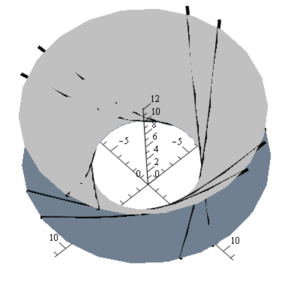
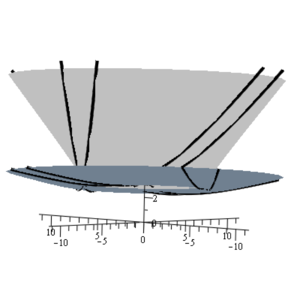
For the model of motion a monatomic gas in space the invariant submodel on a three-dimensional subalgebra consisting of translation operators, dilatation operators and a projective operator is considered, which is reduced to the Abel equation. The paper investigates an approximate solution obtained with the help the asymptotics of integral curves at infinity. This solution describes the vortex motion of a gas, the gas particles move along a plane curves lying on the surface of rotation. The gas spreads and cools down. This solution can be interpreted as a reflection of the incident gas from the wall.
equations of gas dynamics,
projective operator,
invariant submodel,
approximate solution
A system of gas dynamics equations with the monatomic gas state equation is considered. The system admits a fourteen-parameter Lie algebra. A special feature of this algebra is the presence of a projective operator. A three-dimensional subalgebra from the time and space translation operators, Galilean translation operators, dilatation operators, and the projective operator is selected.
The purpose of the research work is to consider the key equation to which an invariant submodel on a selected three-dimensional subalgebra is reduced. For this equation, obtain the asymptotic of integral curves at infinity and investigate the approximate solution obtained.
Methods: To obtain the asymptotic of the solution at infinity, a small parameter is introduced in the key equation. Representing the solution as a series with respect to a small parameter, decomposing the right-hand side of the equation into a series with respect to a small parameter and neglecting the higher terms of the expansion, we obtain a zero approximation.
Results: The solution describes the vortex motion of the gas, the gas particles move along plain curves lying on the surface of rotation. Over time, the gas spreads and cools down. The solution can be interpreted as a reflection of the incident gas from the wall. This solution generalizes the earlier solution obtained for this submodel, which corresponds to the line
Conclusions: The obtained asymptotic will be correct only for a part of the integral curves, as can be seen if we replace variables in the key equation such that an infinitely distant point moves to the origin. This point will be a non-elementary singular point for the equation and, thus, part of the integral curves will have a different asymptotic behavior.