Article outline

Wave processes in granular media occur in various situations, e.g. during the gunpowder combustion or catastrophic events in coal mines and factories, known as dust explosions. Dust explosions are dangerous the fatal events, occurring in the presence of the chemically active dust. Shock waves are generated during such events, enhancing the explosion, even transitioning deflagration to detonation in some cases. Numerical modeling is an extremely valuable tool for understanding of the nature of such processes. The goal of this paper is to present a numerical study of a shock wave interaction with a layer of inert dust.

In this paper the numerical algorithm for modelling high energy wave processes in two-phase media is presented. This algorithm is based on the 2D Baer-Nunziato model and HLLC-like solver. Numerical algorithm includes pressure relaxation substep, which takes into account intergranular stress. This phenomenon is extremely important for qualitatively and quantitatively correct description of the two-phase wave processes in granular media. Interphase momentum transfer is also taken into account. HLLC-like solver is developed for the 2D BN equations for the particular case of phases being near mechanical equilibrium. HLLC solver allows for the better volume fraction discontinuity resolution that HLL method, but simple enough to be extrapolated for the three-phase case in the future work. Overall numerical algorithm is based on the Strang splitting technique with three stages: hyperbolic, pressure relaxation and momentum exchange. For the momentum exchange substep the explicit Euler method is used.

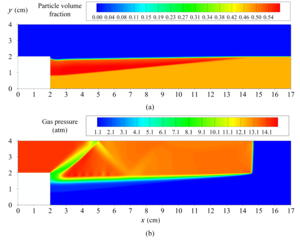
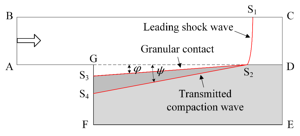
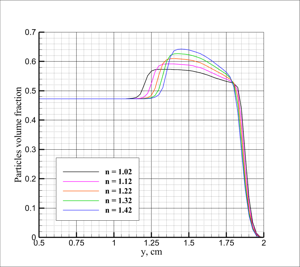
Described numerical algorithm was verified using data for the Rogue shock tube test. The algorithm achieved great qualitative and quantitative agreement with experimental data. After verification, the algorithm was used to simulate the experiment of B.C. Fan on interaction of the passing shock wave with the dust layer. Within the framework of this paper only wave effects inside the dust layer are considered. The effect of dust dispersion are neglected. It is shown in experiment that the layer is deformed by the shock wave, deflecting from the initial level by some angle a₁. Moreover, under this deformed surface is present the compacted layer of the dust. 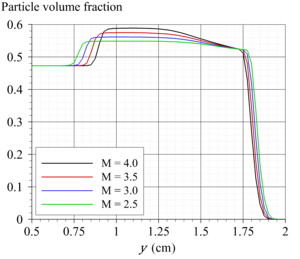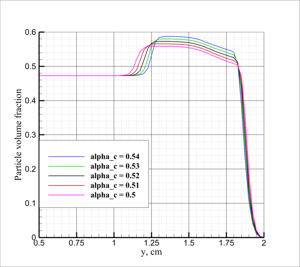This layer propagates at an angle a₂. It is shown that a₁ increases with increase of Mach number of the passing wave, but a₂ decreases. Numerical experiments have shown that the compacted layer of dust acts as a plug, preventing penetration of the pressure wave from the region behind the shock wave inside the dust layer. Obviously with increase of the Mach number, layer is more and more compressed, increasing the effectiveness of the compaction plug. The parametric study was conducted, which confirmed the leading role of the plug in the formation of the flow inside the dust layer, and shed some light onto the dust compaction mechanism itself.

In the current paper, the robust and simple numerical algorithm for multiphase flow modeling is presented. This algorithm is verified and used to analyze inner structure of the compressed dust layer. The obtained results show agreement with the experimental data and are used to suggest an explanation to the experimentally known phenomenon.