Yulmukhametova Yu.V.
Deformation of a gas ball into a needle or disk. Multiphase Systems. 19 (2024) 2. 59–63 (in Russian).
Deformation of a gas ball into a needle or disk
Yu.V. Yulmukhametova
Ufa University of Science and Technology, Ufa, Russia,
Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia
Abstract
One model of gas motion is considered, the particle velocities of which linearly depend on spatial coordinates. The model consists of two
first-order matrix differential equations, two first-order vector differential equations, a gas equation of state and a density function. An exact
solution for the antidiagonal linearity matrix has been found for this model. All components of the velocity vector have been determined. The
equations of the world lines of motion of gas particles are written down. The motion of the isolated volume of gas particles is investigated.
Keywordslinear velocity field,
uniform deformation,
gas dynamics,
exact solution
Article outline
Objective: to find and study new exact solutions to the equations of ideal gas dynamics with a linear velocity field.
Methods: the following approach was chosen to find new accurate solutions. The linearity matrix is chosen in an anti-diagonal form with various elements. After substituting such a solution into the ordinary differential equations of the model, the form of these matrix elements is determined.
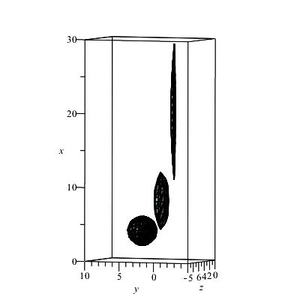
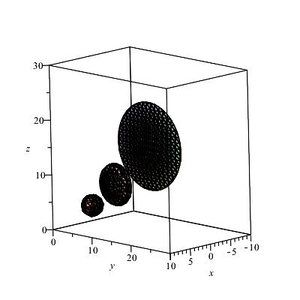
Result: The type of the linearity matrix made it possible to determine the type of all gas dynamic functions. Speed, density and pressure. The equations of the world lines of gas particles are found. The movement of the allocated volume is constructed.
References
- Чандрасекхар С. Эллипсоидальные фигуры равновесия. М.: Мир, 1973. 288 с.
Chandrasekhar S. Ellipsoidal Figures of Equilibrium. New Haven and London: Yale University Press. 1969. 252 p.
- Riemann B. Ein Beitrag zu den Untersuchungen uber die Bewegung einer flussigen gleichartigen Ellipsoides. Abh. d. Konigl. Gesell. der Wiss. zu
Gottingen, 1861.
- Борисов А.М., Мамаев И.С. Динамика жидких и газовых эллипсоидов. М.–Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт
компьютерных исследований, 2010. 364 с.
Borisov A.V., Mamaev I.S. (eds.) Dinamika zhidkikh i gazovykh ellipsoidov [Dynamics of liquid and gas ellipsoids]. Moscow, Izhevsk: Institut
komp’yuternykh issledovanii Publ., 2010. 364 p. (in Russian)
- Овсянников Л.В. Лекции по основам газовой динамики. М.–Ижевск: Институт компьютерных исследований, 2003. 336 с.
Ovsyannikov L.V. Lektsii po osnovam gazovoi dinamiki [Lectures on the fundamentals of gas dynamics]. Moscow; Izhevsk: Institut Komp’yuternykh
Issledovanii, 2003. 336 p. (in Russian)
- Уразбахтина Л.З., Юлмухаметова Ю.В. Плоский коллапс газа с линейным полем скоростей // Тр. Ин-та математики и механики УрО РАН. 2023.
Т. 29, № 2. С. 207–216.
Urazbakhtina L.Z., Yulmukhametova Yu.V. A planar collapse of a gas with a linear velocity field // Trudy Instituta Matematiki i Mekhaniki URO RAN.
2023. Vol. 29, No. 2. Pp. 207–216. (in Russian)
- Yulmukhametova Yu. Solution with a linear velocity field for a submodel of one-dimensional gas motions // Journal of Applied Mechanics and
Technical Physics. 2016. Volume 57, Issue 1. P. 3–10.
- Юлмухаметова Ю.В. Решение гидродинамической подмодели ранга 2 с линейным полем скоростей // Челябинский физико-математический
журнал. 2021. Т. 6, вып. 3. С. 321–330.
Yulmukhametova Yu. The solution of a hydrodynamic submodel of rank 2 with a linear velocity field // Chelyabinsk Physico-Mathematical Journal.
2021. V. 6, is. 3. С. 321–330. (in Russian)
DOI: 10.47475/2500-0101-2021-16306[8]
- Nikonorova R., Siraeva D., Yulmukhametova Y. New Exact Solutions with a Linear Velocity Field for the Gas Dynamics Equations for Two Types of State
Equations // Mathematics. 2022. V. 10(1). P. 123.
DOI: 10.3390/math10010123
- Гумеров И.И., Каташова А.А., Юлмухаметова Ю.В. Коллапсирующие движения двухатомного газа, плотность которого зависит только от
времени // Многофазные системы. 2023. Т. 18, № 1. С. 9–16.
Gumerov I.I., Katashova A.A., Yulmukhametova Yu. Collapsing motions of a diatomic gas, the density of which depends only on time // Multiphase
systems. 2023. V. 18, No. 1. P. 9–16. (in Russian)
DOI: 10.21662/mfs2023.1.002
- Юлмухаметова Ю.В. Подмодели газовой динамики с линейным полем скоростей // Сибирские электронные математические известия. 2012. Т. 9.
С. 208–226.
Yulmukhametova Yu.V. Submodels in gas dynamics with linear field of velocity // Journal Siberian Electronic Mathematical Reports. 2012. Vol. 9.
Pp. 208–226. (in Russian)
EDN: puabwb
- Уразбахтина Л.З. Интегрируемые гидродинамические подмодели с линейным полем скоростей // Сибирский журнал индустриальной
математики. 2012. Т. 15, № 3(51). С. 135–145.
EDN: noukts
Urazbakhtina L. Z. Integrable hydrodynamic submodels with a linear velocity field // Journal of Applied and Industrial Mathematics, 2013, vol. 7,
no. 1. pp. 117–126.
DOI: 10.1134/S1990478913010110
- Хабиров С.В. Аналитические методы в газовой динамике. Уфа: БГУ. 2013. 224 с.
Khabirov S.V. Lectsii. Analiticheskie metody v gazovoi dinamike [Lections. Analytical methods in gas dynamics], Ufa, Bashkir State Univ. 2013, 224 p.
(in Russian)