Recently, special attention is paid to the development of deposits of natural gas hydrates due to their wide distribution in nature and the large reserves of hydrocarbons contained in such deposits. The article discusses an innovative gas extraction method based on the injection of carbon dioxide into a gas hydrate formation. This technology makes it possible to accumulate greenhouse gases in solid gas hydrate form at very low economic costs, as well as solve the problem of natural gas extraction. A mathematical model of non-isothermal filtration of carbon dioxide in the gaseous state, methane and water is constructed based on methods and equations of mechanics of multiphase media considering the replacement of methane in the gas hydrate with carbon dioxide to obtain predictive calculations. The model additionally takes into account such important factors as filtration flow of water and gas, real gas properties, Joule–Thomson and adiabatic compression effects; the process of CH4 –CO2 replacement in gas hydrate is assumed to be equilibrium. The equations are presented to calculate the values of the main process parameters (pressure, temperature, mass fraction of gas phase components, phase saturations, etc.) in one-dimensional radial axisymmetric approximation. Discrete analogues of differential equations are written down and an algorithm for numerical solution of the proposed mathematical model is given. Calculation of saturation distributions of methane and carbon dioxide hydrates is carried out considering their phase equilibrium at current values of pressure, temperature and water saturation. Numerical solutions are constructed that describe the distributions of pressure, temperature, mass concentrations of gas phase components and saturations of methane and carbon dioxide hydrates in the reservoir for the problem of injecting carbon dioxide into a reservoir initially saturated with methane and its hydrate.
mathematical model,
filtration,
replacement of methane in gas hydrate with carbon dioxide,
algorithm of solution
Purpose:
Mathematical modeling of the process of injection of carbon dioxide into an underground reservoir initially filled with methane and its hydrate needs to be carried out to study the simultaneous process of replacing methane in its hydrate with carbon dioxide. This method is considered more advantageous compared to such “classic” methods as lowering pressure, increasing temperature or using inhibitors due to the simultaneous possibility of both natural gas production and carbon dioxide sequestration in the reservoir. The importance of the latter is undeniable due to the need to reduce greenhouse gas emissions, one of which is carbon dioxide.
Methodology for solving this problem needs to be developed to carry out predictive calculations and obtain the distributions of main parameters such as pressure, temperature, mass fraction of gas phase components, phase saturations and etc. This allows studying the influence of some initial parameters on the process of injection of gaseous carbon dioxide and subsequently the extraction of substituted natural gas obtained from underground storage facilities.
Methodology:
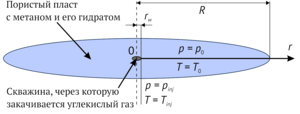
A mathematical model of non-isothermal filtration of carbon dioxide in the gaseous state was constructed using methods and equations of multiphase media. The porous formation is considered to be initially saturated with methane and its hydrate, the pressure and temperature gives the conditions for stable existence of methane hydrate. The problem is considered in a one-dimensional radial axisymmetric formulation. Carbon dioxide is injected through the well at constant pressure and temperature at which carbon dioxide is in a gaseous state and its hydrate can form.
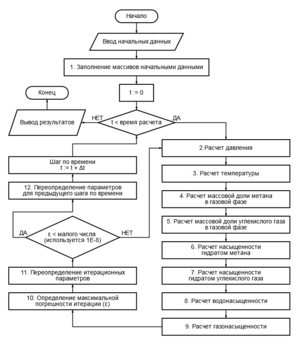
Discrete analogues of the equations of the mathematical model are constructed.
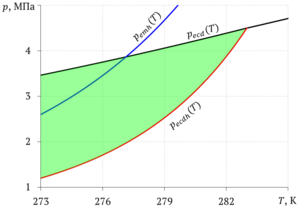
Discrete analogues of the equations to calculate pressure, temperature and mass fraction of methane in the gas phase are solved using an implicit scheme using the Thomas algorithm. Water saturation is calculated explicitly (IMPES method), and the mass fraction of carbon dioxide in the gas phase and gas saturation are also explicitly calculated. Methane and carbon dioxide hydrate saturations are calculated using the phase transition equilibrium condition.
The entire system of equations is solved by simple iteration method. In this case, the parameters calculated at earlier steps of the algorithm are used in calculating parameters at later steps of the algorithm. The algorithm for solving the considered system of equations of the mathematical model is presented in the form of a flow chart.
Findings:
A mathematical model of non-isothermal filtration of gas and water is presented considering the formation/decomposition of methane and carbon dioxide hydrates, as well as an algorithm for solving the equations of the presented mathematical model.
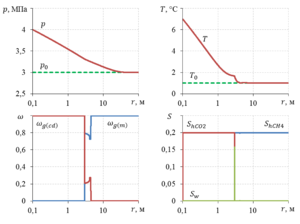
Numerical solutions were constructed for the one-dimensional plane-radial case, describing the distributions of pressure, temperature, mass concentrations of gas phase components and saturations with methane and carbon dioxide hydrates in the underground reservoir.
Three zones can be distinguished with considered values of the initial parameters: in the first zone of the formation, the one close to the carbon dioxide injection boundary, the pores are saturated with carbon dioxide and its hydrate; further, the gas phase, water and gas hydrate are present in the pores of the formation; in the third zone the pore volume is occupied by methane and its hydrate. There is also a joint filtration of carbon dioxide and methane in some area of the formation.
The constructed temperature distribution also demonstrates that the process of replacing methane with carbon dioxide in methane hydrate is exothermic since near the front of the replacement process the temperature exceeds initial reservoir temperature.
Originality/value:
The mathematical model proposed in the paper adequately describes the studied process of carbon dioxide replacement in methane gas hydrate. The model considers the filtration of gas and water phases simultaneously; methane and carbon dioxide gases can also mix.
The second zone of all the zones of the formation, where water is present in a free state, is negligible in size (in calculations, the length was about 1 cm). Therefore, the frontal mode of the process of replacing methane with gaseous carbon dioxide takes place. Due to the insignificant size of the second zone, the solubility of carbon dioxide in water can be ignored in the mathematical model.