E.Sh. Nasibullaeva
Theoretical analysis of linear oscillations of bubbles in a polydisperse cluster. Multiphase Systems. 19 (2024) 1. 7–17 (in Russian).
Theoretical analysis of linear oscillations of bubbles in a polydisperse cluster
E.Sh. Nasibullaeva
Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia
Abstract
The dynamics of a single air bubble in an unbounded liquid are significantly different from the dynamics of an individual bubble in clusters
due to the hydrodynamic interaction between the bubbles. Studying the mechanism of this interaction is one of the important aspects
in the study of the fundamental nature of acoustic and hydrodynamic cavitation. In this work, to analyze small oscillations of bubbles in
a spherical cluster near a stable equilibrium position, the mathematical theory of a linear conservative system with several degrees of
freedom is applied to explain the mechanism of interaction between bubbles of different sizes. Using this theory, in the general case, it has
been proven that the number of resonance frequencies in a polydisperse cluster coincides with the number of fractions. It is shown that in
the regions of the main resonance (at low frequencies) bubbles of different fractions oscillate in phase, and in the regions of secondary
resonances (at high frequencies) the phases successively change to the opposite, starting with the fraction containing bubbles of the
largest radius, and further changing in order of decreasing. Using the example of a two-fraction cluster, it was found that there is an
inertial connection between the bubbles, but there is no force connection; when the number of bubbles of one of the fractions is small, the
connection between them and the bubbles of the other fraction is weak, while the interaction between them can be strong. An analysis of
the energy transfer between bubbles of different fractions showed that the change in the nature of bubbles oscillations in the fraction with
a small radius, while the nature of vibration of bubbles in the other fraction does not change, is the result of dynamic damping.
Keywordsbubble cluster,
amplitude-frequency characteristics,
linear conservative system with several degrees of freedom,
natural frequency of oscillations,
resonance,
partial system,
dynamic damping
Article outline
The single bubble dynamics in a boundless liquid differs significantly from the dynamics of a individual bubble in clusters (called bubble cloud or bubble cluster in the literature) due to the hydrodynamic interaction between bubbles. Studying the mechanism of this interaction is one of the important aspects in studying the fundamental nature of acoustic and hydrodynamic cavitations. All theoretical works based on the assumption of the thermal nature of cavitations can be divided into two groups according to the approaches used in their studies: 1) analysis of the macroscopic motion of a bubble cluster by averaging the equations of conservation of momentum and mass of liquid and gas, when the mixture of liquid and gas bubbles is considered as continuous environment; 2) analysis of microscopic movements of individual bubbles in a cluster. In this work, the dynamics of spherical gas bubbles in a polydisperse cluster is analytically studied in the case of small oscillations of the bubbles based on a mathematical model of a bubble cluster developed by the author within the framework of the second approach. In accordance with this model, a polydisperse cluster was considered as a large drop containing liquid and a large number of microbubbles of different sizes, and the bubbles in the cluster were conditionally divided into a finite number of fractions, where each fraction was characterized by the initial radius of the bubbles.
The main goal of this work is to explain the mechanism of interaction between bubbles of different sizes in a polydisperse cluster under the influence of an external field.
Methodology. The mathematical theory of a linear conservative system with several degrees of freedom is applied to the analysis of bubble oscillations in a cluster near a stable equilibrium position.
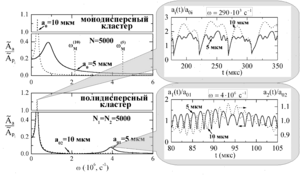
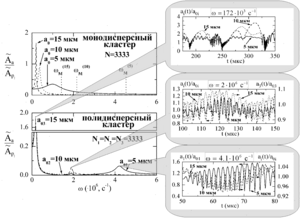
Findings. Based on the amplitude-frequency characteristics obtained earlier by the author, corresponding graphs were constructed for two- and three-fraction clusters. It was shown, that
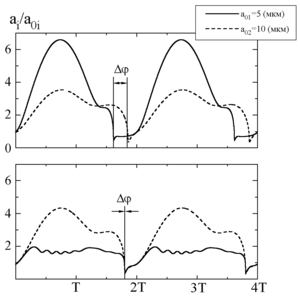
- in addition to the main resonance in the low-frequency region, there are secondary resonances at higher frequencies, and the number of these resonances is 1 less than the number of fractions. In the region of the main resonance, bubbles of different fractions oscillate in phase, and in the regions of secondary resonances, the phases successively change to the opposite, starting with the fraction containing bubbles of the largest radius, and then change in descending order;
- there is an inertial connection between the bubbles, but there is no force connection;
- with a small number of bubbles of one fraction, the connection between them and the bubbles of another fraction is weak, but the interaction between them can be strong.
Originality. Using the theory of a linear conservative system with several degrees of freedom, in the general case it has been proven that the number of resonant frequencies in a polydisperse cluster coincides with the number of fractions, and the nature of the oscillations of bubbles of different fractions (in phase or antiphase) in different resonant regions has been explained. An analysis of the energy transfer between bubbles of different fractions showed that a change in the nature of oscillations of bubbles in a fraction with a small radius (without changing the nature of vibration of bubbles in another fraction) is the result of dynamic damping.
References
- Nasibullaeva E.S., Akhatov I.S. Bubble cluster dynamics in an acoustic field // J. Acoust. Soc. Am. 2013. V. 133, No. 6. P. 3727–3738.
DOI: 10.1121/1.4802906
- Hsieg D.Y., Plesset M.S. On the propagation of sounds in a liquid containing gas bubbles // Phys. Fluids. 1961. V. 4, No. 8. P. 970–975.
DOI: 10.1063/1.1706447
- Wijngaarden L. On the equations of motion for mixtures of liquid and gas bubbles // J. Fluid. Mech. 1968. V. 33, No. 3. P. 465–474.
DOI: 10.1017/S002211206800145X
- Biesheuvel A., Wijngaarden L. Two-phase flow equation for a dilute dispersion of gas bubbles in liquid // J. Fluid Mech. 1984. V. 148. P. 301–318.
DOI: 10.1017/S0022112084002366
- Ishii M. Thermo-fluid dynamic theory of two-phase flow. Paris: Eyrolles. 1975. 248 p.
- Нигматулин Р.И. Динамика многофазных сред. Ч. I. М.: Наука. 1987. 464 с.
Nigmatulin R.I. Dynamics of Multiphase Media. New York: Hemisphere, 1991, vol. 1. P. 360.
- Nakoryakov V.E., Pokusaev B.G., Shreiber I.R. Wave Propagation in Gas–Liquid Media. New York: Begell House. 1993. Chap. 3. Pp. 53–90.
DOI: 10.1017/S0022112094224515
- Wijngaarden L. On the collective collapse of a large number of cavitation bubbles in water // Proc. 11th Internetional Congress of Applied Mechanics,
Munich, 1964, ed. H. Görtler, Springer Verlag. 1964. P. 854–865.
DOI: 10.1007/978-3-662-29364-5_112
- Hansson I., Kedrinskii V.K., Mørch K.A. On the dynamics of cavity clusters // J. Phys. D: Appl. Phys. 1982. V. 15, No. 9. P. 1725–1734.
DOI: 10.1088/0022-3727/15/9/017
- Hansson J., Mørch K.A. The dynamics of cavity clusters in ultasonic (vibratory) cavitation erosion // J. Appl. Phys. 1980. V. 51, No. 9. P. 4651–4658.
DOI: 10.1063/1.328335
- Kanthale P.M., Gogate P.R., Pandit A.B., Wilhelm A.M. Cavity cluster approach for quantification of cavitational intensity in sonochemical reactors //
Ultrason. Sonochem. 2003. V. 10, No. 4–5. P. 181–189.
DOI: 10.1016/S1350-4177(03)00088-9
- Fuster D., Colonius T. Modelling bubble clusters in compressible liquids // J. Fluid Mech. 2011. V. 688. P. 352–389.
DOI: 10.1017/jfm.2011.380
- Omta R. Oscillations of a cloud of bubbles of small and not so small amplitude // J. Acoust. Soc. Am. 1987. V. 82, No. 3. P. 1018–1033.
DOI: 10.1121/1.395376
- D’Agostino L., Brennen C.E. Acoustical absorption and scattering cross sections of spherical bubble clouds // J. Acoust. Soc. Am. 1988. V. 84, No. 6.
P. 2126–2134.
DOI: 10.1121/1.397058
- D’Agostino L., Brennen C.E. Linearized dynamics of spherical bubble clouds // J. Fluid Mech. 1989. V. 199. P. 155–176.
DOI: 10.1017/S0022112089000339
- Smereka P., Banerjee S. The dynamics of periodically driven bubble clouds // Phys. Fluids. 1988. V. 31, No. 12. P. 3519–3531.
DOI: 10.1063/1.857559
- Birnir B., Smereka P. Existence theory and invariant manifolds of bubble clouds // Commun. Pure Appl. Maths. 1990. V. 43, No. 3. P. 363–413.
DOI: 10.1002/cpa.3160430304
- Daemi M., Taeibi-Rahnt M., Massah H. Study of acoustic bubble cluster dynamics using a lattice Boltzmann model // Chinese Physics B. 2015. V. 24,
No. 2. P. 024302.
DOI: 10.1088/1674-1056/24/2/024302
- Аганин А.А., Давлетшин А.И. Гидродинамическое взаимодействие слабонесферических газовых пузырьков в жидкости в трёхмерной
постановке задачи // Труды Института механики им. Р.Р. Мавлютова Уфимского научного центра РАН. 2017. Т. 12, № 1. С. 51–58.
Aganin A.A., Davletshin A.I. Hydrodynamic interaction of weakly nonspherical gas bubbles in a liquid in the three-dimensional problem statement.
Proceedings of the Mavlyutov Institute of Mechanics. 2017. V. 12, No. 1. P. 51–58 (in Russian).
DOI: 10.21662/uim2017.1.008
- Аганин А.А., Давлетшин А.И. Деформации взаимодействующих газовых пузырьков в жидкости при акустическом воздействии // Ученые записки
Казанского университета. Серия: физико-математические науки. 2018. Т. 160, № 4. C. 657–669.
Aganin A.A., Davletshin A.I. [Deformation of interacting gas bubbles in liquid under acoustic excitation]. Uchenyye zapiski Kazanskogo universiteta.
Seriya Fiziko-matematicheskiye nauki. 2018. V. 160, No. 4. P. 657–669 (in Russian).
EDN: yyjckn
- Аганин А.А., Давлетшин А.И., Халитова Т.Ф. Численное моделирование динамики пузырьков в центральной области стримера // Многофазные
системы. 2018. Т. 13, № 3. С. 11–22.
Aganin A.A., Davletshin A.I., Khalitova T.F. Numerical simulation of bubble dynamics in central region of streamer. Multiphase Systems. 2018. V. 13,
No. 3. P. 11–22 (in Russian).
DOI: 10.21662/mfs2018.3.002
- Qinghim N. Acoustic cavitation characteristics of mixed bubble groups composed of different types of bubbles // Acta Phys. Sin. 2020. V. 69, No. 18.
P. 184301.
DOI: 10.7498/aps.69.20200381
- Chahine G.L., Duraiswami R. Dynamical interaction in a Multi–Bubble Cloud // J. Fluids Eng. 1992. V. 114, No. 4. P. 680–686.
DOI: 10.1115/1.2910085
- Takahira H., Akamatsu T., Fujikawa S. Dynamics of a Cluster of Bubbles in a Liquid (Theoretical Analysis) // JSME Int. J. Ser. B. 1994. V. 37, No. 2. P. 297–
305.
DOI: 10.1299/jsmeb.37.297
- Skaropoulos N.C., Yagridou H.D., Chrissoulidis D.P. Interactive resonant scattering by a cluster of air bubbles in water // J. Acoust. Soc. Am. 2003. V. 113,
No. 6. P. 3001–3011.
DOI: 10.1121/1.1572141
- Akhatov I., Konovalova S. Structure formation in acoustic cavitation // Multiphase Sci. Technol. 2005. V. 17, No. 4. P. 343–371.
DOI: 10.1615/MultScienTechn.v17.i4.30
- Doinikov A.A. Mathematical model for collective bubble dynamics in strong ultrasound fields // J. Acoust. Soc. Am. 2004. V. 116, No. 2. P. 821–827.
DOI: 10.1121/1.1768255
- Ilinskii Y.A., Hamilton M.F., Zabolotskaya E.A. Bubble interaction dynamics in Lagrangian and Hamiltonian mechanics // J. Acoust. Soc. Am. 2007.
V. 121, No. 2. P. 786–795.
DOI: 10.1121/1.2404798
- Yasui K., Iida Y., Tuziuti T., Kozuka T., Towata A. Strongly interacting bubbles under an ultrasonic horn // Physical Review E. 2008. V. 77. P. 016609.
DOI: 10.1103/PhysRevE.77.016609
- LV L., Zhang H., Cui B., Chen L., Luo X. The Numerical Investigation on Bubble Interaction Dynamics in Hydrodynamic Cavitation // MECHANIKA. 2021.
V. 27, No. 2. P. 115–121.
DOI: 10.5755/j02.mech.26187
- Насибуллаева Э.Ш., Ахатов И.Ш. Динамика пузырькового кластера в акустическом поле // Акуст. ж. 2005. Т. 51, № 6. С. 709–717.
EDN: hsinhv
Nasibullaeva E.Sh., Akhatov I.Sh. Dynamics of a bubble cluster in an acoustic field. Acoustical Physics. 2005. V. 51, No. 6. P. 705–712.
DOI: 10.1134/1.2130902
- Nigmatulin R.I., Akhatov I.Sh., Vakhitova N.K., Nasibullaeva E.Sh. Dynamics of bubble clusters // in Nonlinear Acoustics at the Turn of the Millenium
(AIP conference proceedings), Melville, New York, USA. 2000. V. 524, No. 1. P. 455–460.
DOI: 10.1063/1.1309263
- Мандельштам Л.И. Лекции по теории колебаний. М.: Наука. 1972. 470 с.
Mandelstam L.I. Lectures on the Theory of Oscillations. Moscow: Nauka. 1972. P. 470 (in Russian).
- Нигматулин Р.И., Ахатов И.Ш., Насибуллаева Э.Ш., Вахитова Н.К. Динамика пузырьковых кластеров // Вестник БашГУ. Уфа. 1999. № 2. C. 12–15.
Nigmatulin R.I., Akhatov I.Sh., Nasibullaeva E.Sh., Vakhitova N.K. [Dynamics of bubble clusters]. Vestnik bashkirskogo universiteta [Bulletin of the
Bashkir State University]. 1999. No. 2. P. 12–15 (in Russian).
- Пановко Я.Г. Введение в теорию механических колебаний. М.: Наука. 1980. 272 с.
Panovko Ya.G. Introduction to the theory of mechanical vibrations. Moscow: Nauka. 1980. P. 272 (in Russian).