ISSN 2658–5782
DOI 10.21662
Electronic Scientific Journal


© Институт механики
им. Р.Р. Мавлютова
УФИЦ РАН

Яндекс.Метрика web site traffic statistics

Gumerov I.I., Katashova A.A., Yulmukhametova Y.V. Collapsing motions of a diatomic gas whose density depends only on time. Multiphase Systems. 18 (2023) 1. 9–16 (in Russian).
2023. Vol. 18. Issue 1, Pp. 9–16
URL: http://mfs.uimech.org/mfs2023.1.002,en
DOI: 10.21662/mfs2023.1.002
Collapsing motions of a diatomic gas whose density depends only on time
Gumerov I.I.∗, Katashova A.A.∗, Yulmukhametova Y.V.∗∗
∗Ufa University of Science and Technology, Ufa, Russia
∗∗Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia

Abstract

One submodel of gas motion with a linear velocity field is considered in the paper. Namely, a submodel that defines the movements of a polytropic gas with a density that depends only on time. A polytropic gas is a gas for which the internal energy is a function linear in temperature. The submodel under consideration is given by a system of ordinary differential equations of the 22nd order for unknown functions. These functions characterize the movements of gas particles and determine the type of density, pressure and entropy functions. The exact solution is sought for a special case, namely for a diagonal linearity matrix. Two new exact solutions have been found. The type of vector functions of velocity, density and pressure are determined. 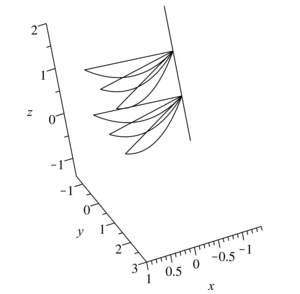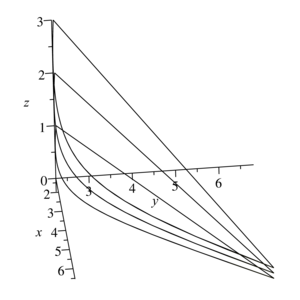By the form of the velocity function, the world lines of motion of gas particles are recorded. In the three-dimensional space of coordinates x, y, z, the trajectories of gas particles for various initial data are constructed. A qualitative analysis of the movement was carried out. The Jacobi matrix is constructed. The moments of collapse of gas particles are determined by the value of the Jacobian. Both solutions have collapse: collapse on a straight line and collapse at a point.

Keywords

polytropic gas,
diatomic gas,
linear velocity field,
inhomogeneous deformation,
trajectories of gas particles,
world lines of particle motion,
Jacobian

Article outline

Objective: to find and study new exact solutions to the equations of gas dynamics with a linear velocity field and time-dependent density.

Methods: The following approach was chosen to find new exact solutions. The linearity matrix is selected in a diagonal form with several identical elements. After substituting such a solution into the ordinary differential equations of the model, the form of these matrix elements is determined.

Result: The type of the linearity matrix allowed us to determine the type of all gas-dynamic functions. Velocity, density, pressure and entropy.

References

  1. Dirichlet G.L. Untersuchunger uber eih Problem der Gydrodynamik // J. Reine Angew. Math. 1860. Vol. 58. P. 181.
  2. Riman B. [Essays] Sochinenia. M.-L.: GITTL, 1948. Pp. 339-366 (In Russian).
  3. Ovsannikov L.V. [New solution of hydrodynamic equations] Novoe reshenia uravnenia gidrodinamili // DAN USSR. 1956. Vol. 111, No 1. Pp. 47–49 (In Russian).
  4. Dyson J.F. Dynamics of a spinning gas cloud // J. Math. Mech. 1968. Vol. 18, No. 1. Pp. 91–101.
    DOI: 10.1512/iumj.1969.18.18009
  5. Giron J.F., Ramsey S.D., Baty R.S. Nemchinov-Dyson Solutions of the Two-Dimensional Axisymmetric Inviscid Compressible Flow Equations // Phys. Fluids. 2020. Vol. 32. 127116.
    DOI: 10.1063/5.0032170
  6. Guo Y., Hadžić M., Jang J. Continued Gravitational Collapse for Newtonian Stars // Arch. Rational Mech. Anal. 2021. Vol. 239. Pp. 431-–552.
    DOI: 10.1007/s00205-020-01580-w
  7. Nikonorova R., Siraeva D., Yulmukhametova Y. New Exact Solutions with a Linear Velocity Field for the Gas Dynamics Equations for Two Types of State Equations // Mathematics. 2022. Vol. 10, Issue 1. 123.
    DOI: 10.3390/math10010123
  8. Yulmukhametova Yu.V. Solution of ideal gas equations describing Galilean invariant motions with helical level lines, with collapse on a helicoid // Vest. Sam. state tehn. univ. Ser. phys.-mat. science. 2019. Vol. 23, No 4. Pp. 797–808 (in Russian).
    DOI: 10.14498/vsgtu1703
  9. Yulmukhametova Yu.V. [Submodels of gas dynamics with a linear velocity field]Podmodeli gazovoi dinamiki s lineinim polem scorostey : dissertation ... Candidate of Physical and Mathematical Sciences : 01.01.02 / Yulmukhametova Yulia Valeryevna; [Place of defense: Ufa Scientific Center of the Russian Academy of Sciences]. Ufa, 2011. 118 p.
  10. Ovsyannikov L.V. [Lectures on the fundamentals of gas dynamics] Lektsii po osnovam gazovoy dinamiki. M.-Izhevsk: komp’yuternykh issledovaniy. 2003. 336 p. (in Russian).