Delev V.A.
The topological soliton decay in a linear defect of the domain structure of twisted nematic. Multiphase Systems. 17 (2022) 3–4. 135–144 (in Russian).
The topological soliton decay in a linear defect of the domain structure of twisted nematic
Delev V.A.
IMCP UFRC RAS, Ufa, Russia
Abstract
In this paper, the topological soliton decay in an oscillating linear defect of electroconvective structure (Williams
domains) arising in π/2 twisted nematic liquid crystal are studied. In contrast to planarly oriented nematics,
hydrodynamic flows in the domains of a twisted nematic have a helical character. Since, in addition to the tangential
velocity component, there is also axial component, the direction of which is opposite in neighboring domains. This
feature leads to the formation of stable localized extended objects — linear defects oriented normal to Williams
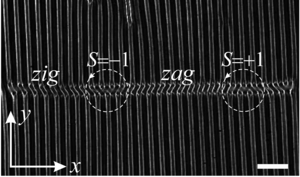
domains. With increasing applied voltage, “zig-zag” oscillations occurs in linear defects. The boundaries between
the “zig” and “zag“ states are classical dislocations. It has been found, that the dislocation, moving along the core
of the defect, breaks up into an antidislocation and two dislocations. Unlike case of planarly oriented nematics,
dislocations are not isolated from each other by unperturbed rolls but remain “bound” by hydrodynamic flows within
the core of a linear defect. It is assumed that the splitting of the dislocation occurs as a result of the local instability
of the orientational twist mode of the director n due to its strong coupling with the hydrodynamic velocity. In
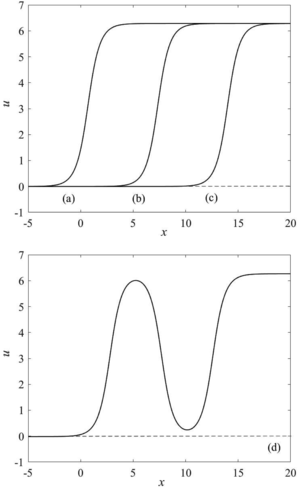
the framework of the sine–Gordon equation, in the presence of a dissipative term and spatial perturbations, the
mechanism of a topological soliton (kink) decay into antisoliton and two solitons is considered.
Keywordsnematic liquid crystal,
nematic,
electroconvection,
Williams domains,
twist mode,
linear defect,
dislocation,
sine–Gordon equation,
kink
Article outline
The decay of a topological soliton in an oscillating linear defect of a domain structure (Williams domains) that arises in the electroconvection
system of π/2 twisted nematic liquid crystal (NLC) is studied. In contrast to planarly oriented NLCs, hydrodynamic flows in the domains of a twisted nematic are helicoidal in nature,
since, in addition to the tangential velocity component, there is also an axial component, the direction of which is opposite in neighboring domains. This feature leads to the formation
of stable extended stationary objects — linear defects oriented normally to the Williams domains. With increasing applied voltage, zig-zag domain oscillations appear in linear
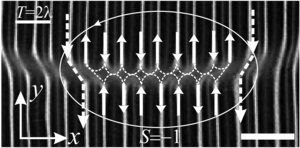
defects. The boundaries between zig and zag states are classical dislocations with topological charges S = ±1 (topological solitons — kinks). It was found that
a dislocation with S = +1, moving along the linear defect core of a certain length, can decay into an antidislocation with S = –1 and two dislocations with S = +1.
The resulting single dislocations do not separate from each other, as in the case of a planar orientation of NLC, but remain “bound” by hydrodynamic flows within the linear defect core.
It is assumed that the splitting of a dislocation occurs as a result of the local instability excitation of the orientational twist mode of the director n (n is a unit
vector, indicates the direction of the predominant molecules orientation in the NLC layer) in dislocation core due to the strong coupling between director orientation and hydrodynamic
flow velocity in NLC. The local instability of the orientational twist mode of the director n in the dislocation core (instability in the kink internal mode) arises when the
hydrodynamic flows moving through the linear defect core become non-stationary and zig-zag domain oscillations arise. At the same time, the Williams domain structure remains stationary.
The further dynamics of dislocations is set in such a way that the continuity of the helicoidal flow of an anisotropic liquid is ensured in the nonstationary linear defect core.
An attempt is made to qualitatively explain the topological soliton – kink decay by the excitation of its internal mode instability in the framework of the perturbed sine-Gordon equation.
It should be emphasized that the investigation of the transition from regular defect motion to highly nonstationary spatiotemporal dynamics remains a challenge in modern science.
This phenomenon is related to defect-mediated turbulence. Kinks, like vortices and spirals, are particular cases of a more general phenomenon called topological defects. Although these
objects may possess different origin and nature in different physical systems, they all possess very similar dynamical properties. In this work, it has been found that the transition
process to weak turbulence (defects mediated turbulence) in the electroconvection system of π/2 twisted NLCs occurs not only due to the dislocations creation and annihilation, but also
by their “elementary” decay into an antidislocation and two dislocations. Such instabilities as the solitons decay or breakup can adversely affect various processes in technology,
medicine, etc. In particular, one possible mechanisms that is currently believed to be responsible for the transition from tachycardia to ventricular fibrillation in the heart muscle
is the spontaneous breakup of a single spiral wave of electrical activity into multiple spirals leading to a turbulent wave behavior. Therefore, it is very important to understand not
only all possible mechanisms of soliton decay in order to learn how to avoid them, but also, if possible, to control them.
References
- Coullet P., Gil L., and Lega J. Defect-mediated turbulence // Physical Review Letters. 1989. V. 62, No. 14. Pp. 1619–1622.
DOI: 10.1103/PhysRevLett.62.1619
- Cross M.C., Hohenberg P.C. Pattern formation outside of equilibrium // Reviews of Modern Physics. 1993. V. 65. Pp. 851–1112.
DOI: 10.1103/RevModPhys.65.851
- Getling A.V. Rayleigh-Benard convection. M.: Editorial URSS, 1999. 248 s. (In Russian)
- Blinov L.M. Electro-Optical and Magneto-Optical Properties of Liquid Crystals (Nauka, Moscow, 1978; Wiley, New York, 1983). 384 p.
- Pikin S.A. Strukturnye prevrashcheniya v zhidkih kristallah. M.: Nauka, 1981. 336 s. (In Russian)
- De Gennes P.G. and Prost J. The Physics of Liquid Crystals. Oxford: Clarendon, 1994. 596 p.
- Buka A. and Kramer L. (editors). Pattern Formation in Liquid Crystals. N.Y.: Springer-Verlag, 1996. 339 p.
- Kuramoto Y. Phase dynamics of weakly unstable periodic structures // Progress of Theoretical Physics. 1984. V. 71, No. 6. Pp. 1182–1196.
DOI: 10.1143/PTP.71.1182
- Toulouse G., Kléman M. Principles of a classification of defects in ordered media // Journal de Physique Lettres. 1976. V. 37, No. 6. Pp. 149–
151.
DOI: 10.1051/jphyslet:01976003706014900
- Eckmann J.-P., Goren G. and Procaccia I. Nonequilibrium nucleation of topological defects as a deterministic phenomenon // Physical
Review A. 1991. V. 44, No. 2. Pp. 805–808.
DOI: 10.1103/PhysRevA.44.R805
- Kai S., Chizumi N., and Kohno M. Pattern formation, defect motions and onset of defect chaos in the electrohydrodynamic instability of
nematic liquid crystals // Journal of the Physical Society of Japan. 1989. V. 58. Pp. 3541–3554.
DOI: 10.1143/JPSJ.58.3541144
Multiphase Systems
- Rasenat S., Steinberg V., and Rehberg I. Experimental studies of defect dynamics and interaction in electrohydrodynamic convection //
Physical Review A. 1990. V. 42, No. 10. Pp. 5998–6008.
DOI: 10.1103/PhysRevA.42.5998
- Bodenschatz E., Weber A., and Kramer L. Interaction and dynamics of defects in convective roll patterns of anisotropic fluids // Journal
of Statistical Physics 1991. V. 64, No. 5. Pp. 1007–1015.
DOI: 10.1007/BF01048810
- Joets A. and Ribotta R. Localized bifurcations and defect instabilities in the convection of a nematic liquid crystal // Journal of Statistical
Physics 1991. V. 64, No. 5/6. Pp. 981–1005.
DOI: 10.1007/BF01048809
- Delev V.A., Toth P., and Krekhov A.P. Electroconvection in twisted nematic liquid crystals // Molecular Crystals and Liquid Crystals. 2000.
V. 351. Pp.179–186.
DOI: 10.1080/10587250008023267
- Tatsumi S., Sano M., and Rossberg A.G. Observation of stable phase jump lines in convection of a twisted nematic liquid crystal //
Physical Review E. 2006. V. 73. Pp. 011704-1–8.
DOI: 10.1103/PhysRevE.73.011704
- Hertrich A., Krekhov A.P., and Scaldin O.A. The electrohydrodynamic instability in twisted nematic liquid crystals // Journal de Physique
II (France). 1994. V. 4. Pp. 239–252.
DOI: 10.1051/jp2:1994126
- Braun O.M., Kivshar’ YU.S. Model’ Frenkelya-Kontorovoj. Koncepcii, metody, prilozheniya. M.: Fizmatlit, 2008. 536 s. (In Russian)
- Dodd R., Ejlbek Dzh., Gibbon Dzh., Morris H. Solitony i nelinejnye volnovye uravneniya. M.: Mir, 1988. 694 s. (In Russian)
- Zabusky N.J., Kruskal M.D. Interaction of solitons in a collisionless plasma and recurrence of initial states // Physical Review Letters.
1965. V. 15, No. 6. P. 240–243.
DOI: 10.1103/PhysRevLett.15.240
- Kerner B.S., Osipov V.V. Autosolitons // Uspehi Fizicheskih Nauk. 1989. V. 157, No. 2. Pp. 201–266. (In Russian)
- Rosanov N.N. Spatial hysteresis and optical patterns. Berlin: Springer, 2002. 308 p.
- Lam L., Prost J (editors). Solitons in liquid crystals. N.Y.: Springer Science & Business Media, 1992. 338 p.
- Shen Yu. and Dierking I. Recent progresses on experimental investigations of topological and dissipative solitons in liquid crystals //
Crystals. 2022. V. 12, No. 1. Pp. 1–17.
DOI: 10.3390/cryst12010094
- CHuvyrov A.N., Skaldin O.A., Delev V.A., Lebedev YU.A., Batyrshin E.S. Struktura i dinamika dislokacij Frenkelya-Kontorovoj pri
elektrokonvekcii v zhidkih kristallah // ZHurnal Eksperimental’noj i Teoreticheskoj Fiziki. 2006. T. 130, № 6. S. 1072–1081. (In Russian)
eLIBRARY ID: 9430706
- Skaldin O.A., Delev V.A., Shikhovtseva E.S., Lebedev Yu.A., and Batyrshin E.S. Breatherlike defects and their dynamics in the one-
dimensional roll structure of twisted nematics // Journal of Experimental and Theoretical Physics. 2015. V. 121, No. 6. Pp. 1082–1095.
DOI: 10.1134/S1063776115120158
- Delev V.A., Nazarov V.N., Scaldin O.A., Batyrshin E.S., and Ekomasov E.G. Complex dynamics of the cascade of kink–antikink interactions
in a linear defect of the electroconvective structure of a nematic liquid crystal // Journal of Experimental and Theoretical Physics. 2019.
V. 110, No. 9. Pp. 607–612.
DOI: 10.1134/S0021364019210069
- Delev V.A. Inelastic interactions of solitons in a linear defect of the electroconvective structure of a nematic liquid crystal // Letters to
Journal of Experimental and Theoretical Physics. 2021. Vol. 113, No. 1. Pp. 23–29.
DOI: 10.1134/S0021364021010021
- González J.A., Bellorín A., Guerrero L.E. Internal modes of sine-Gordon solitons in the presence of spatiotemporal perturbations //
Physical Review E. 2002. V. 65. Pp. 065601-1-4.
DOI: 10.1103/PhysRevE.65.065601
- González J.A., Bellorín A., Guerrero L.E. Kink-soliton explosions in generalized Klein–Gordon equations // Chaos. Solitons & Fractals.
2007. V. 33. Pp. 143–155.
DOI: 10.1016/j.chaos.2006.10.047
- Kivshar Yu.S. and Malomed B.A. Dynamics of solitons in nearly integrable systems // Reviews of Modern Physics. Vol. 61, No. 4. 1989.
Pp. 763–915.
DOI: 10.1103/RevModPhys.61.763
- Bak P. and Brazovsky .A. Theory of quasi-one-dimensional conductors: Interaction between chains and impurity effects // Physical
Review B. 1978. V. 17, No. 8. Pp. 3154–3164.
DOI: 10.1103/PhysRevB.17.3154
- Zipes D.P., Jalife J, and Stevenson W.G. Cardiac electrophysiology: from cell to bedside. E-Book, 2017. 1120 p.
- González J.A., Bellorín A., Guerrero L.E. Controlling soliton explosions // Physics Letters A. 2005. V. 338. Pp. 60–65.
DOI: 10.1016/j.physleta.2005.02.018