Analytical review of investigations aimed at studying the aqueous foam behavior under the shock-wave impact is given. The main approaches and theoretical approximations used in the development of aqueous foams models are analyzed. The two-phase gas-drop model of aqueous foam is considered, based on the laws of conservation of mass, momentum, and energy in accordance with one-pressure, two-velocity, two-temperature approximations. The model describes foam dynamics under a high - intensity impact, which destroys the foam structure into microdroplets, and takes into account interfacial heat transfer, interfacial drag and virtual mass forces and the phenomenon of foam syneresis (deposition). The numerical implementation of the model was carried out using new solvers in the OpenFOAM software. The analysis of the numerical solution of the spherical explosion in aqueous foam is given for the conditions of the literature experimental data. The syneresis influence on the intensity and velocity of shock wave propagation is shown. The two-phase model of aqueous foam is considered, which takes into account its elastic- viscous-plastic properties for conditions of weak impact that does not destroy foam structure. The model takes into account the elastic properties of aqueous foam at small deformations and describes it as a non-Newtonian fluid when the foam changes its state from the elastic to viscoplastic. The weak shock wave propagation dynamics in the layer of aqueous foam with the formation of a two-wave structure, consisting of the main wave and the elastic precursor ahead of it, is analyzed. The process of local aqueous foam compaction zone formation, followed by a gaseous region, behind the shock wave front is shown. The reliability of the obtained results of numerical studies is confirmed by their agreement with the literature experimental data
shock wave,
aqueous foam,
OpenFOAM software,
mathematical and numerical modeling
Purpose. Review of existing aqueous foam models and investigations analysis of the strong and weak shock waves dynamics in aqueous foam, taking into account the rheological features of its behavior depending on the intensity of the impact.
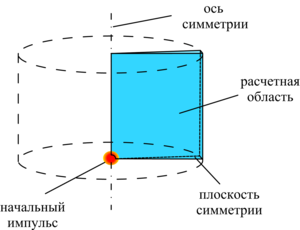
Methodology. In the considered works, the assumption about the foam structure destruction into microdroplets by a strong shock wave was used, which made it possible to apply the gas-droplet model in the single-pressure, two-velocity, two-temperature approximations to describe the dynamics of aqueous foam, taking into account the interfacial interaction forces, heat transfer processes, and the phenomenon of foam syneresis. When studying the interaction of aqueous foams with weak shock waves, a two-phase model was used, taking into account the foam elastic properties by Hooke's law and viscoplastic flow above the von Mises yield critical value - by the Herschel-Bulkley model. To describe the properties of air and water, the equations of state in the form of Peng-Robinson and Mie-Gruneisen are used. The applied models are numerically implemented using the finite volume method by creating and compiling new solvers in the OpenFOAM software.
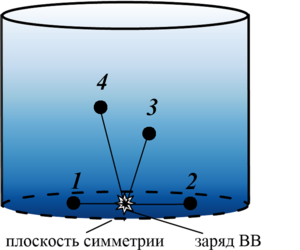
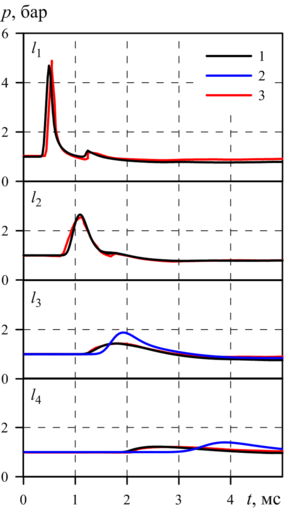
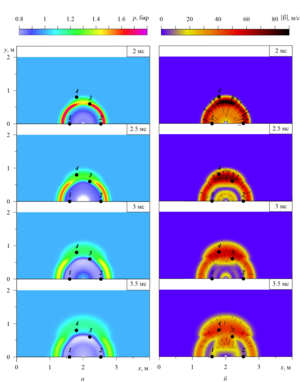
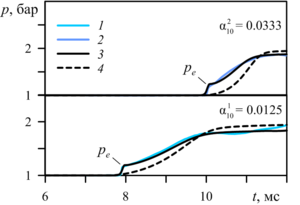
Findings. In the works noted in the review, numerical study of the powerful spherical explosion dynamics in aqueous foam based on the gas-droplet foam model was performed for the experimental data of E. Del Prete et al. It is shown, that the process of foam syneresis leads to the shock wave front velocity increase in the vertical upward direction due to the foam upper layers density reduction during its deposition. The comparative analysis of the calculated and experimental pressure oscillograms in the shock wave at the positions of the sensors showed, that the numerical solutions, taking into account the foam syneresis, have the best agreement with the experimental data of E. Del Prete et al., and the calculations relative error does not exceed 4%.
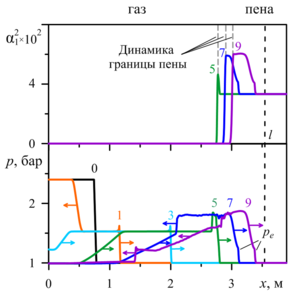
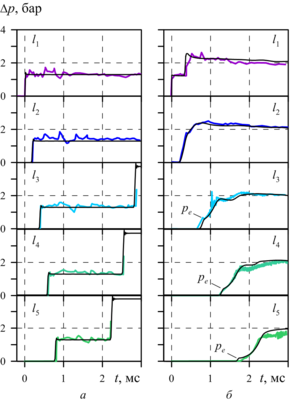
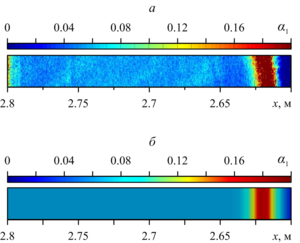
In the next reviewed paper, the elastic-viscous-plastic model of aqueous foam is considered for the numerical study of the dynamics of weak air shock waves in a layer of aqueous foam under the experimental data conditions of G. Jourdan et al. and M. Monloubou et al. Numerical solutions in the form of pressure profiles demonstrate a two-wave configuration of the shock pulse in the foam: the main compression wave is ahead of the elastic low-amplitude precursor. Comparative analysis of numerical solutions for the presence of a foam layer in the shock tube showed a decrease in the velocity of the shock pulse front by a factor of 2.5 compared to the gas. The impact of a shock wave on the foam layer leads to the formation of a local zone of increased liquid volume fraction, located behind the front of the shock wave.
Agreement between calculations and experimental data G. Jourdan et al. and M. Monloubou et al. confirms the reliability of the obtained numerical solutions.
Value. The review provides the analysis of existing aqueous foam models that describe its behavior under shock-wave impact.
The two-phase gas-droplet mixture model is considered for studying the dynamics of strong shock waves in aqueous foam in accordance with one-pressure, two-velocity, two-temperature approximations, taking into account interfacial heat transfer, interfacial drag force, virtual mass force, and the phenomenon of foam syneresis. It is shown that foam syneresis leads to increase in the shock wave propagation in the vertical upward direction due to the density reduction of the upper foam layers.
The aqueous foam dynamics under the influence of weak shock wave, which do not destroy its structure, is analyzed. The elastic-viscous-plastic behavior of aqueous foam is described in terms of a two-phase mixture model. Elastic properties are taken into account in accordance with Hooke's law. The transition to a viscoplastic flow was controlled by the von Mises yield criterion, and above the critical yield value - by the Herschel - Bulkley law for a non-Newtonian fluid.
The causes for the two-wave structure of the shock wave, which consists of the elastic precursor ahead of the main compression wave, are detailed. Features of the increased liquid volume fraction region formation beyond the shock wave front, behind which there is the foam-free zone formed as a result of the foam boundary movement following the shock wave, are revealed.
Numerical implementation of the models was carried out using new solvers of the OpenFOAM software. There is a satisfactory agreement between the calculations and experimental data.