Article outline

Purpose. Comparative analysis of the numerical and self-similar solutions of the Sedov problem on a point explosion in gas.

Methodology. For the numerical solution the sonicFoam solver of the OpenFOAM library is chosen, which is built on the implicit PISO algorithm that calculates pressure with a two-step corrector. In accordance with the mathematical formulation of the problem the computational grid region was formed in a spatial Cartesian coordinate system, the initial and boundary conditions of the problem were set using the setFieldsDict and blockMeshDict utilities. The boundary conditions for pressure, temperature, and velocity as a function of time are generated using the uniformFixedValue function. For numerical modeling the system of differential equations of gas dynamics including the equations of continuity, Navier-Stokes motion for a compressible medium and conservation of internal energy is used.

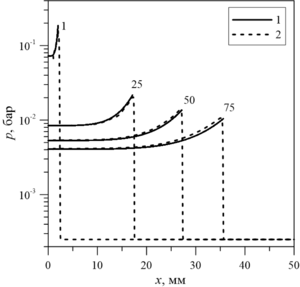
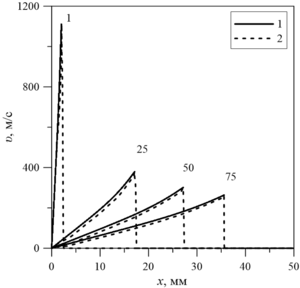
Findings. The analytical solution to the Sedov’s problem was obtained under the under the following initial conditions: gas-nitrogen with an initial density ρ₁=0.0125 kg/m³, explosion energy E=100 J, adiabatic index γ=1.4. In the numerical implementation of a similar problem using the sonicFoam solver, the following values were used to describe the unperturbed state: p=6 Pa, T=25 K. When calculating the internal energy of the gas, the isobaric heat capacity of nitrogen was chosen c_p = 1039 J/(kg·K). The computational domain was divided on 2500 cubic cells. The values of pressure, temperature, and velocity as a function of time in accordance with the obtained analytical solutions for the values of the coordinate x=1 mm at the left boundary of the region were set. For this, the boundary conditions p(t), T(t), v(t) were specified as a table function depending on the time t in accordance with the type of the uniformFixedValue boundary condition of the sonicFoam solver,. On the right boundary of the computational domain, the condition of free flow (type zeroGradient) was used. The lateral boundaries were determined by the slip condition (slip type). At result of comparing the obtained analytical and numerical solutions using the sonicFoam solver of the OpenFOAM package, a satisfactory agreement of the solutions presented in the form of pressure and mass velocity profiles in the considered time ranges is obtained.

Value. Comparative analysis of analytical and numerical solutions for the problem of a point explosion in the plane case (Sedov's problem) is perfomed. The consistency of the solutions obtained analytically and using the sonicFoam solver of the OpenFOAM package with the initial and boundary conditions constructed on the basis of the investigated self-similar solution is shown. The need for such a comparative analysis is important for evaluating the reliability of the obtained solutions for a wide range of gas-dynamic problems using the considered solver.