ISSN 2658–5782
DOI 10.21662
Electronic Scientific Journal


© Институт механики
им. Р.Р. Мавлютова
УФИЦ РАН

Яндекс.Метрика web site traffic statistics

Golubev Yu.F., Melkumova E.V. Transfer by a Manipulator with a Three-finger Grasp of a Brittle Cylinder. Multiphase Systems. 14 (2019) 3. 202–207.
2019. Vol. 14. Issue 3, Pp. 202–207
URL: http://mfs.uimech.org/mfs2019.3.026
DOI: 10.21662/mfs2019.3.026
Transfer by a Manipulator with a Three-finger Grasp of a Brittle Cylinder
Golubev Yu.F.∗,∗∗, Melkumova E.V.∗∗
∗Keldysh Institute of Applied Mathematics, RAS, Moscow
∗∗M.V. Lomonosov State University, Moscow

Abstract

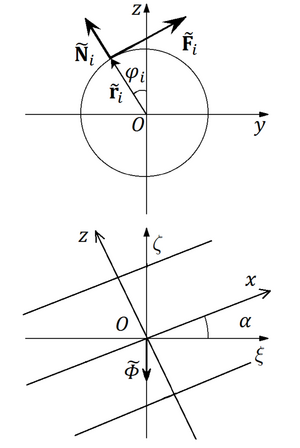
We consider the problem of the brittle cylinder grasping by the n fingers of the robot-manipulator. Each finger contacts the cylinder in a single supporting point with Amontons-Coulomb or for two footholds spinning friction. Using numerical simulations and analytically, possible locations of contact points on the cylinder, for which there is a kinetostatics problem solution when the cylinder is moved by three fingers, are received. By the analogy of the equilibrium of a three-legged robot on a cylinder for the problems of transfer by a manipulator with a three-finger grasp of a cylinder or for a robot on a surface which legs suspension points are on a cylinder surface. Two supporting points can be on one diameter in the cylinder base. Or because of friction on the opposite sides of the robot center of mass or giving in the dynamics, it is point C. The analogy of the problem is oscillations in the vicinity of the stable equilibrium one cylinder on another. The cylinder lies on one finger rectangular to it, of the hand of a hu-manoid robot, adheres to the end of the other finger. Similarly holds the glass. Robot can hold the horizontal cylinder by three fingers. Let one of the points is in vertical plane containing cylinder axis and another are in the plane orthogonal to the axis. The supporting points are on the external surface of the lower semi-cylinder and the cylinder center mass is in the footholds triangle. The supporting set is divided into two subsets.

Keywords

three-finger grasp,
Amontons-Coulomb friction,
three-legged robot

This work was supported by the Russian Foundation for Basic Researches (grant no. 19 − 01 − 00123 A).

References

  1. Lensky, A.V., Lizunov, A.V., Mozhzhevelov, S.B. and etc. Control of the manipulator along communication // Bulletin of the USSR Academy of Sciences. Solid mechanics. 1987. V. 57, No. 5. Pp. 41–49.
  2. Okhotsimski, D.E., Golubev, Yu.F. Mechanics and Motion Control of Automatic Locomotion Apparatus. Moscow. Nauka Publishers. 1984. (in Russian.)
  3. Beletski, V.V. Two-legged Locomotion. Model Dynamics and Control Problems. Moscow. Nauka Publishers. 1984 (in Russian.)
  4. Chernousko, F.L. Equilibrium conditions for a solid on a rough plane. Izvestiya RAN, ser. Solid Mechanics. 1988. No. 6. Pp. 6–17. (in Russian).
    https://elibrary.ru/item.asp?id=25761712
  5. Bolotnik N.N., Chernousko F.L. Parameter optimization for a tube-crawling robot. Izvestiya RAN, ser. Solid Mechanics. 1995. No. 6. Pp. 27–41 (in Russian).
    https://elibrary.ru/item.asp?id=26050814
  6. Pfeiffer F., Rossmann T., Chernousko F.L., Bolotnik N.N. Optimization of Structural Parameters and Gaits of a Pipe-Crawling Robot. In: Bestle D., Schiehlen W. (eds) IUTAM Symposium on Optimization of Mechanical Systems. Solid Mechanics and its Applications, vol 43. 1996. Pp. 231–238.
    DOI: 10.1007/978-94-009-0153-7_29
  7. Golubev, Yu.F.: The Fundamentals of Theoretical Mechanics. Moscow State University. 2019. 728 p. (in Russian).
  8. Golubev, Yu.F., Melkumova, E.V. Static-Stability Conditions for a Walking Apparatus in Horizontal Cylinder and on Two Planes. Journal of Computer and Systems Sciences International. Robotics. 1999. Vol. 38, No 2. Pp. 278–284 (Translated from Izvestiya Akademii Nauk. Teoriya i Sistemy Upravleniya. 1999. No 2. Pp. 116–122.
    https://elibrary.ru/item.asp?id=13318257
  9. Golubev, Yu.F., Melkumova, E.V. On Stability of Equilibrium Positions for Walking Robot in a Smooth Horizontal Tube. Proc. of the Third International Conference on Climbing and Walking Robots. Madrid, Spain. 2000. Pp. 433–440.
  10. Golubev, Yu.F., Melkumova, E.V. Equilibrium Problem for a Two-Legged Robot on Rough Horizontal Cylinder Taking into Account the Reaction Components Along the Cylinder Axis. Moscow, Russia: MAKS Press. 2010. 61 p. (in Russian).
  11. Golubev, Yu.F., Melkumova, E.V. Walking Robot Dynamics on a Rough Inclined Cylinder. In 8-th European Solid Mechanics Conference, Book of Abstracts. Graz. 2012. Pp. 1–2.
  12. Golubev, Yu.F., Melkumova, E.V. Prescribed Motion of a Two-legged Walking Robot on a Rough Cylinder. Proc. of the 2016 International Conference “Stability and Oscillations of Nonlinear Control Systems” (Pyatnitskiy’s Conference). Moscow. 2016. Pp. 1–4.
    DOI: 10.1109/STAB.2016.7541184
  13. Golubev, Yu.F., Melkumova, E.V. The Existence of Solution for Robot Motion on a Cylinder Pipe. All-Russian Meeting of University Lecturers and Department Heads on Theoretical Mechanics, Robotics and Mechatroinics. 2016. Pp. 30–33. (in Russian).
  14. Golubev, Yu.F., Melkumova, E.V. Footholds Admissible Areas Structure Properties for a Two-legged Walking Robot on an Inclined Cylinder. In the Lomonosov Readings. Mechanics Section. Moscow. 2017. Pp. 64–65. (in Russian).
  15. Golubev, Yu.F., Melkumova, E.V. Footholds Admissible Areas Structure of a Two-legged Walking Robot on an Inclined Cylinder. Abstracts of International Scientific Conference Fundamental and Applied Problems of Mechanics, Dedicated to the 170th Anniversary of a Distinguished Russian Scientist N.E. Zhukovsky. Bauman Moscow State Technical University. 2017. Pp. 83–84. (in Russian).
  16. Golubev, Yu.F., Melkumova, E.V. Two-legged Walking Robot Prescribed Motion on a Rough Cylinder. AIP Conference Proceedings. 2018. V. 1959. 030009.
    DOI: 10.1063/1.5034589
  17. Golubev, Yu.F., Melkumova, E.V. An Analogy of the Equilibrium of a Two-legged Robot on a Cylinder for the Problem of Transfer by a Manipulator With a Two-finger Grasp of a Cylinder. Proceedings of XLVI Summer School-Conf. “Advanced Problems in Mechanics”. St. Petersburg, Russia. 2018. Pp. 117–124.
    http://www.ipme.ru/ipme/conf/APM2018/Proceedings-2018.html
  18. Golubev, Yu.F., Melkumova, E.V. Footholds Admissible Areas Structure of a Two-legged Walking Robot on an Inclined Cylinder. IOP Conference Series: Materials Science and Engineering. 2018. V. 468. 012003.
    DOI: 10.1088/1757-899X/468/1/012003