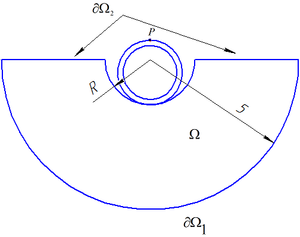
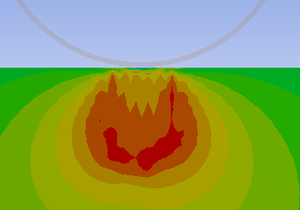
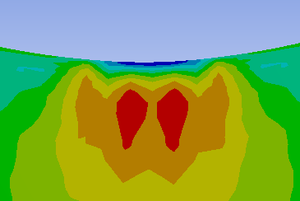
The article deals with the problem of pressing the steel cylindrical shell into the elastoplastic half-space having a cylindrical concavity. The calculation and analysis of the stress-strain state of the steel shell and elastoplastic half-space. Given the dependence of the shear half-space, the safety factor and stress state in steel shell from the force pushing the shell in the half-space. The calculations were carried out for three radii of concavities and two types of half-space materials. It was assumed that the elastoplastic half-space obeys the Mohr-Coulomb fracture criterion.
elastoplastic deformation,
Mohr–Coulomb failure criterion,
associative plastic flow rule,
contact problem
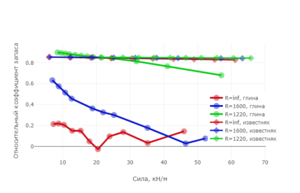
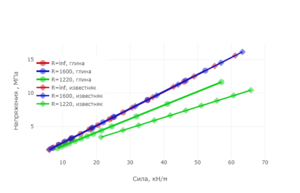
Problem: determination of the stress state of the steel shell and the elastoplastic half-space having a spherical concavity when the shell is pressed into the half-space.
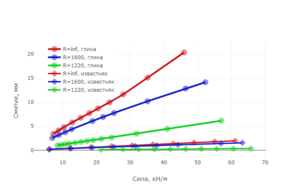
Method: Three variants of the radius of concavities and two variants of the elastoplastic material of the half-space (clay and limestone) were considered. As a result of the research it was found that:
1) Plastic deformation in the half-space do not occur for forces of the indentation does not exceed 70 kN/m. Except in the case of clay half-space, having the concavity of infinite radius.
2) Stresses in soil and pipeline do not reach critical values.
3) The effect of indentation in the half-space on the stress state of the steel shell is quite small. Equivalent stresses in the shell do not exceed 10% of the yield strength of steel 13G1S-U.