Arkhipov V.A., Basalaev S.A., Kostyushin K.V., Usanina A.S.
Experimental study of the surfactant effect on the dynamics of bidispersed bubble cluster. Multiphase Systems. 2025;20(3):135–144 (in Russian).
Experimental study of the surfactant effect on the dynamics of bidispersed bubble cluster
V.A. Arkhipov, S.A. Basalaev, K.V. Kostyushin, A.S. Usanina
🖂National Research Tomsk State University, Tomsk, Russia
Abstract
The article presents the results of an experimental study of the process of ascent of a cluster consisting of bubbles of two different sizes in
a volume of liquid unlimited by walls in the presence and absence of surfactant in a liquid medium in the ranges of Reynolds numbers
Re = 200 ÷ 600 and Re = 0.1 ÷ 50. The effect of the concentration of the surfactant and the cluster parameters (initial concentration, ratio
of the number and diameters of bubbles in the cluster) on the qualitative picture of ascent and the velocity of the bidispersed bubble
cluster is analyzed. The condition for the existence of the cluster of bidispersed bubbles is experimentally established.
Keywordsbidispersed bubble cluster,
surfactant,
qualitative picture of ascent,
cluster velocity,
experimental study
Article outline
Problem: experimental identification of the patterns of the process of unconstrained ascent of cluster of bidispersed air bubbles in the presence and absence of surfactants in the range of Reynolds numbers Re = 0.1 ÷ 600.
Methods: method of experimental study based on the visualization of the process using modern high-speed video filming techniques.
In a study was determined:
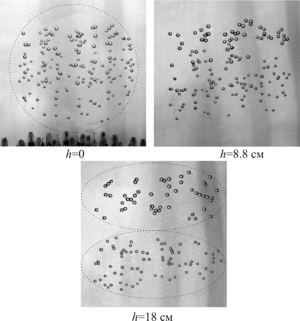
1. In distilled water (Re > 200), a bidispersed spherical bubble cluster separates into two monodispersed clusters during the ascent process at a distance h*
from the place of its formation, regardless of the presence of surfactants. The key difference is in the ascent velocity of the resulting clusters: in pure liquid, the condition
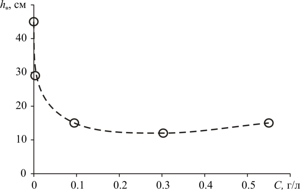
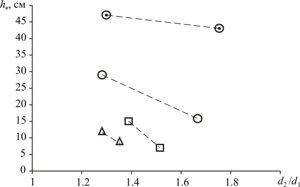
u1 < u2 is met, while in a surfactant solution, u1 < u2. It has been experimentally confirmed
that the separation distance h* monotonically decreases with an increase in both the surfactant concentration and the dimensionless parameter d2/d1.
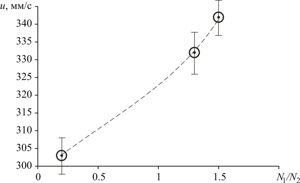
The dependence of the rising velocity of the bidispersed cluster on the composition of the medium and the parameters of the cluster was revealed. In distilled water (in the absence of surfactants),
the cluster velocity monotonically increases with an increase in both the ratio of the number of bubbles N1/N2 and the initial volume concentration of the gas.
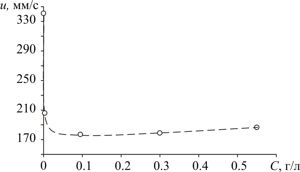
On the contrary, the introduction of surfactant into the system leads to decrease in the ascent velocity, and this decrease increases with an increase in the concentration of the surfactant.
2. An experimental study of contact rising in glycerol (Re < 50) showed that the stable existence of the bidispersed bubble cluster is possible in two ranges of parameters: with a diameter
ratio of 1.56 < d2/d1 < 1.82 and a predominance of small bubbles (N1 ≫ N2,
where the proportion of large bubbles does not exceed 6%); with d2/d1 > 1.56 and a predominance of large bubbles
(N1 < N2, where the proportion of small bubbles is less than 30%).
The stability of the cluster under these conditions is due to the interaction of the hydrodynamic fields of the bubbles. In contrast, during contactless ascent as well as during contact
ascent with a ratio of d2/d1 > 2.13 and a proportion of large bubbles of no more than 6% the bidispersed cluster is not formed; instead, independent ascent of two monodispersed formations is observed.
References
- Левич ВГ. Физико-химическая гидродинамика. М.: Государственное издательство физико-математической литературы; 1959. 700 с.
Levich VG. Physical and chemical hydrodunamics. M.: Gosudarstvennoe izdatel'stvo fiziko-khimicheskoy literaturi; 1959. 700 p. (in Russian)
- Clift R, Grace JR, Weber M. Bubble, drops and particles. London: Academic Press; 1978. 380 p.
- Филиппов ГА, Салтанов ГА, Кукушкин АН. Гидродинамика и тепломассообмен в присутствии ПАВ. М.: Энергоатомиздат; 1988. 184 с.
Filippov GA, Saltanov GA, Kukushkin AN. Hydrodynamics and heat and mass transfer in the presence of surfactants. M.: Energoatomizdat; 1988. 184 p. (in Russian)
- Griffith R. The effect of surfactants on the terminal velocity of drops and bubbles. Chemical Engineering Science. 1962;17:1057–1070.DOI: 10.1016/0009-2509(62)80084-0
- Davis R, Acrivos A. The influence of surfactants on the creeping motion of bubbles. Chemical Engineering Science. 1966;21:681–685. DOI: 10.1016/0009-2509(66)80017-9
- Bel Fdhila R, Duineveld PC. The effect of surfactants on the rise of a spherical bubble at high Reynolds and Peclet numbers. Physics of Fluids. 1996;8:310–321. DOI: 10.1063/1.868787
- Takemura F. Adsorption of surfactants onto the surface of a spherical rising bubble and its effect on the terminal velocity of the bubble. Physics of Fluids. 2005;17(4):048104. DOI: 10.1063/1.1879712
- Zhang Y, Finch A. A note on single bubble motion in surfactant solutions. Journal of Fluid Mechanics. 2001;429:63–66. DOI: 10.1017/S0022112000002755
- Духин СС, Буйков МВ. Теория динамического адсорбционного слоя движущихся сферических частиц. Журнал физической химии. 1964;38(12):3011–3013.
Dukhin SS, Buikov MV. Theory of dynamic adsorption layer of moving spherical particles. Russian Journal of Chemical Chemistry A. 1964;38(12):3011–3013. (in Russian)
- Bratukhin YuK, Kostarev KG, Viviani A, Zuev AL. Experimental study of Marangoni bubble migration in normal gravity. Experiments in Fluids. 2005;38(5):594–605. DOI: 10.1007/s00348-005-0930-7
- Архипов ВА, Васенин ИМ, Усанина АС. Динамика всплытия пузырька в присутствии
поверхностно-активных веществ. Известия РАН. Механика жидкости и газа. 2016;(2):142–151. EDN: VVNQCB
Arkhipov VA, Vasenin IM, Usanina AS. Dynamics of bubble rising in the presence of surfactants. Fluid Dynamics. 2016;51(2):266–274. DOI: 10.1134/S0015462816020137
- Roghair I, Lau YM, Deen NG, et al. On the drag force of bubbles in bubble swarms at intermediate and high Reynolds numbers. Chemical Engineering Science. 2011;66:3204–3211. DOI: 10.1016/j.ces.2011.02.030
- Simonnet M, Gentric C, Olmos E, Midoux N. Experimental determination of the drag coefficient in a swarm of bubbles. Chemical engineering Science. 2007;62:858–866. DOI: 10.1016/j.ces.2006.10.012
- Marrucci G. Communication. Rising Velocity of Swarm of Spherical Bubbles. Industrial and Engineering Chemistry Fundamentals. 1965;5:224–225. DOI: 10.1021/i160014a022
- Olmos E, Gentric C, Vial Ch, Wild G, Midoux N. Numerical simulation of multiphase flow in bubble column reactors. Influence of bubble coalescence and break-up. Chemical Engineering Science. 2001;56:6359–6365. DOI: 10.1016/S0009-2509(01)00204-4
- Zhang L, Zhang J, Deng J. Numerical investigation on the collapse of a bubble cluster near a solid wall. Physical Review E. 2019;99:043108. DOI: 10.1103/PhysRevE.99.043108
- Krishna R, Urseanu MI, Ellenberger J. Rise velocity of a swarm of large gas bubbles in liquids. Chemical Engineering Science. 1999;54:171–183. DOI: 10.1016/S0009-2509(98)00245-0
- Parisien V, Farrell A, Pjontek D, McKnight C, Wiens J. Bubble swarm characteristics in a bubble column under high gas holdup conditions. Chemical Engineering Science. 2017;157:88–98. DOI: 10.1016/j.ces.2016.04.051
- Трушин АМ, Дмитриев ЕА, Носырев МА, Тарасова ТА, Кузнецова ИК. Определение скорости стесненного движения сферических газовых частиц в жидкости в поле силы тяжести. Теоретические основы химической технологии. 2013;47(4):434–440. DOI: 10.7868/S0040357113040167
Trushin AM, Dmitriev EA, Nosyrev MA, Tarasova TA, Kuznetsova IK. Determining the velocity of the hindered motion of spherical gas particles through liquid in a gravity field. Theoretical foundations of chemical engineering. 2013;47(4):368–374. DOI: 10.1134/S0040579513040337
- Takagi S, Toshiyuki O, Masato F, Yoichiro M. Surfactant effect on the bubble motions and bubbly flow structures in a vertical channel. Fluid Dynamics Research. 2009;41(6):065003. DOI: 10.1088/0169-5983/41/6/065003
- Lu J, Corvalan CM, John Chew YM, Huang J-Y. Coalescence of small bubbles with surfactants. Chemical engineering science. 2019;196:493–500. DOI: 10.1016/j.ces.2018.11.002
- Sugiyama K, Takagi S, Matsumoto Y. Multi-scale analysis of bubbly flows. Computer methods in applied mechanics and engineering. 2001;191:689–704. DOI: 10.1016/S0045-7825(01)00309-7
- Струминский ВВ, Гуськов ОБ, Кульбицкий ЮН. Гидродинамика дисперсных и газожидкостных потоков. Доклады Академии Наук СССР. 1984;278(1):65–68. EDN: RUELXT
Struminskii VV, Gus'kov OB, Kul'bitskii YuN. Hydrodynamics of disperse and gas-liquid flows. Soviet Physics. Doklady. 1984;29(9):719–721. EDN: RUEMSN
- Gal-Or B, Waslo B. Hydrodynamics of an ensemble of drops (or bubbles) in the presence or absence of surfactants. Chemical Engineering Science. 1968;23:1431–1446. DOI: 10.1016/0009-2509(68)89053-0
- Архипов ВА, Усанина АС, Басалаев СА, Каличкина ЛЕ, Мальков ВС. Динамика всплытия кластера пузырьков в присутствии поверхностно-активного вещества. Известия РАН. Механика жидкости и газа. 2020;(1):104–112. DOI: 10.31857/S0568528120010028
Arkhipov VA, Usanina AS, Basalaev SA, Kalichkina LE, Mal’kov VS. Dynamics of bubble cluster rising in the presence of a surfactant. Fluid Dynamics. 2020;55(1):103–110. DOI: 10.1134/S0015462820010024
- Lane CD, Parisien V, Macchi A, Donaldson AA. Investigation of bubble swarm drag at elevated pressure in a contaminated system. Chemical Engineering Science. 2016;(152):381–391. DOI: 10.1016/j.ces.2016.06.017
- Mach J, Wiens J, Adjaye J, Donaldson AA, Macchi A. Effect of pressure on the drag coefficient of individual bubbles in a contaminated polydisperse swarm. Chemical Engineering Science. 2020;223:115728. DOI: 10.1016/j.ces.2020.115728
- Crowe CT, Sommerfeld M, Tsuji Y. Multiphase flows with droplets and particles. New York. Washington – London: CRC Press, Boca Raton – Boston. 1998. 327 p.
- Roghair I, Baltussen MW, Van Sint Annaland M, Kuipers JAM. Direct numerical simulations of the drag force of bi-disperse bubble swarms. Chemical engineering science. 2013;95:48–53. DOI: 10.1016/j.ces.2013.03.027
- Goz M, Sommerfeld M. Analysis of bubble interactions in bidisperse bubble swarms by direct numerical simulations. Bubbly flows, analysis, modeling and calculation. Berlin: Springer. 2004:175–190. DOI: 10.1007/978-3-642-18540-3_14
- Serrano-Garcia JC, Mendez-Diaz S, Zenit R. Average properties of bidisperse bubbly flows. Physical Review Fluids. 2018;3(3):034306. DOI: 10.1103/PhysRevFluids.3.034306
- Гуськов ОБ, Струминский ВВ. Динамика дисперсных потоков в присутствии границ. Доклады Академии наук СССР. 1985;285(4):832–835. EDN: RUEKWB
Gus'kov OB, Struminskii VV. Dynamics of disperse streams in the presence of boundaries. Soviet Physics. Doklady. 1985;30(12):995–997. EDN: RUENQT
- Mylyk A, Meile W, Brenn G, Ekiel-Jeżewska ML. Break-up of suspension drops settling under gravity in a viscous fluid close to a vertical wall. Physics of Fluids. 2011;23(6):063302. DOI: 10.1063/1.3600660
- Архипов ВА, Усанина АС, Перфильева КГ, Костюшин КВ, Басалаев СА, Поленчук СН. Способ получения пузырькового кластера заданной конфигурации. Пат. № 2796910 Российская Федерация. 2023.
Arkhipov VA, Usanina AS, Perfilyeva KG, Kostyushin KV, Basalaev SA, Polenchuk SN. Method for obtaining a bubble cluster of a given configuration. Patent № 2796910 The Russian Federation. 2023. (in Russian)
- Архипов ВА, Басалаев СА, Евсеев НС, Костюшин КВ, Усанина АС.
Программа для управления установкой генерации пузырькового кластера заданной конфигурации. Свидетельство о государственной регистрации программы для ЭВМ № 2024685776. Российская Федерация. 2024.
Arkhipov VA, Basalaev SA, Evseev NS, Kostyushin KV, Usanina AS. Program for controlling the installation of generating a bubble cluster of a given configuration. Certificate of state registration of the computer program No. 2024685776 The Russian Federation. 2024. (in Russian)
- Архипов ВА, Усанина АС. Экспериментальное исследование влияния природы поверхностно-активного вещества на динамику всплытия группы монодисперсных пузырьков в маловязкой жидкости. Инженерно-физический журнал. 2024;97(4):874–883. EDN: DAOOTP
Arkhipov VA, Usanina AS. Experimental study of the influence of the nature of a surfactant on the dynamics of rise of a group of monodisperse bubbles in a low-viscosity liquid. Journal of Engineering Physics and Thermophysics. 2024;97(4):859–868. DOI: 10.1007/s10891-024-02955-6
- Борзенко ЕИ, Усанина АС, Шрагер ГР. Экспериментально-теоретическое исследование влияния растворенного поверхностно-активного вещества на динамику всплытия газового пузырька. Известия РАН. Механика жидкости и газа. 2024;(4):108–122. DOI: 10.31857/S1024708424040094
Borzenko EI, Usanina AS., Shrager G.R. Experimental and theoretical investigation of the effect of dissolved surfactant on the dynamics of gas bubble floating-up. Fluid Dynamics. 2024;59(4):741–755. DOI: 10.1134/S0015462824603073
- Борзенко ЕИ, Усанина АС, Шрагер ГР. Влияние поверхностно-активного вещества на скорость всплытия пузырька в вязкой жидкости. Вестник Томского государственного университета. Математика и механика. 2023;84:81–92.
Borzenko EI, Usanina AS, Shrager GR. Effect of surfactant on bubble rising velocity in viscous liquid. Vestnik Tomskogo gosudarstvennogo universiteta. Matematika i mekhanika – Tomsk State University Journal of Mathematics and Mechanics. 2023;84:81–92. (in Russian) DOI: 10.17223/19988621/84/7
- Бошенятов БВ, Гуськов ОБ. Гидродинамическое взаимодействие сферических частиц в потоке невязкой жидкости. Доклады Академии наук. 2011;438(5):626–28. EDN: NWDDIP
Guskov OB, Boshenyatov BV. Hydrodynamic interaction of spherical particles in an inviscid-fluid flow. Doklady Physics. 2011;56(6):352–354. DOI: 10.1134/S1028335811060073
- Архипов ВА, Усанина АС, Чуркин РА. Закономерности всплытия кластера монодисперсных пузырьков в вязкой жидкости в присутствии поверхностно-активного вещества. Теплофизика и аэромеханика. 2023;30:(6):1121–1134. EDN: HMSYDJ
Arkhipov VA, Usanina AS, Churkin RA. Laws of the monodispersed bubble cluster ascent in a viscous liquid in the presence of surfactant. Thermophysics and Aeromechanics. 2023;30(6):1061–1072. DOI: 10.1134/s0869864323060094