In the petrochemical industry, catalytic cracking is used to process heavy petroleum products into lighter fuels. This process is carried
out in catalytic cracking reactors and the result of the process is greatly influenced by the distribution of reagents within the unit, as
well as a number of hydrodynamic parameters such as pressure and temperature. Therefore, computational fluid dynamics methods are
used to model such processes. The paper presents a comparative analysis of various approaches to constructing finite-difference meshes
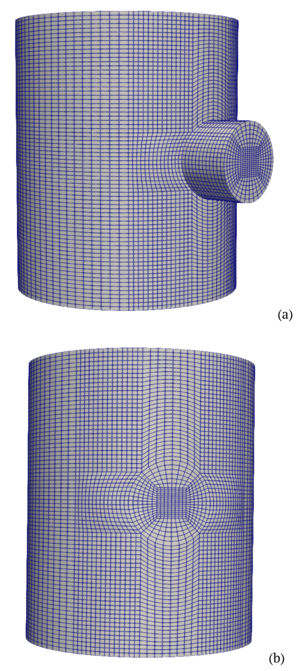
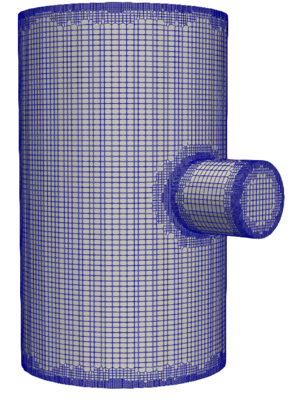
for modeling fluid flow in a T-shaped joint of cylindrical pipes using the OpenFOAM package. Both structured meshes created using
blockMesh and unstructured hexahedral meshes generated by the snappyHexMesh tool are considered. The conducted assessment of
the main quality parameters (non-orthogonality, skewness, cell volume) showed that the structured grid constructed using the improved
block connection scheme provides better orthogonality and skewness indicators compared to the unstructured grid, which has a positive
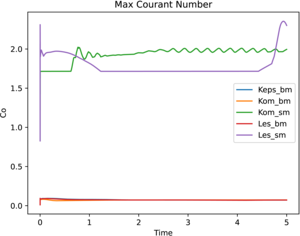
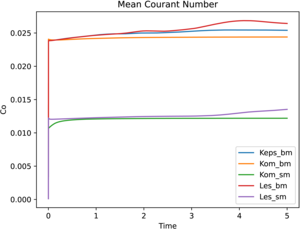
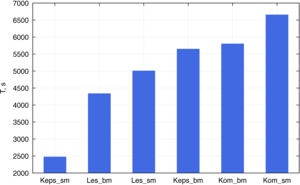
effect on the accuracy and stability of numerical modeling. The results of numerical simulation using different turbulence models (
fluid dynamics,
turbulence,
T-junction,
computational fluid dynamics,
3D mesh,
OpenFOAM
In the petrochemical industry, catalytic cracking is used to process heavy petroleum products into lighter fuel. This process is carried out in catalytic cracking reactors and the result of the process is greatly affected by the distribution of reagents inside the unit, as well as a number of hydrodynamic parameters, such as pressure and temperature. Therefore, computational fluid dynamics methods are used to model such processes. In addition, modeling hydrodynamic flows requires the creation of a high-quality computational grid, especially in the presence of complex geometry, such as cylindrical pipe connections. Within the framework of using the OpenFOAM package, a popular open-source tool for numerical modeling of hydro- and aerodynamics problems, there are several ways to construct a hexahedral (hexagonal) computational grid. For this purpose, the package uses the blockMesh and snappyHexMesh programs, each of which uses different methods for constructing a finite difference grid. In addition, third-party software solutions (Ansys, Salome, FlowVision) can be used to generate grids with subsequent export to the OpenFOAM format.The article examines methods for constructing finite-difference grids for the numerical simulation of turbulent incompressible fluid flow in a T-junction of cylindrical pipes using the OpenFOAM software package. A comparative analysis is carried out between structured grids created with the blockMesh utility and unstructured hexahedral grids generated using snappyHexMesh.
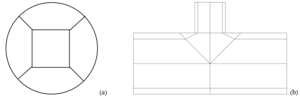
There are different types of computational grids: structured and unstructured. When constructing an unstructured difference grid, the space is divided into irregularly located discrete areas. With such a division, it is impossible to analytically link the grid cell number and its position in space, which allows constructing difference grids for areas of complex shape, but at the same time slows down the calculation when using such grids. In a structured grid, on the contrary, the computational domain is divided into ordered cells. This allows analytically calculating the cell position by its number, which allows more accurate approximation of derivatives; the use of a structured grid leads to acceleration of the computational process with a fixed number of nodal points; a structured grid reduces the amount of computer RAM required for calculations, simplifies the process of spatial decomposition of the computational domain when parallelizing calculations; an orthogonal structured grid reduces the computational error. However, for objects with complex geometry, it is problematic to construct a structured grid, therefore, in practice, unstructured grids are often used in calculations.
The article considers methods for constructing finite-difference meshes for numerical simulation of turbulent incompressible fluid flow in a T-junction of cylindrical pipes using the OpenFOAM software
package. A comparative analysis of structured meshes constructed using the blockMesh utility and unstructured hexahedral meshes obtained using snappyHexMesh is carried out. Geometric approaches to
constructing meshes for complex intersection areas of pipes of different diameters are studied. An analysis of mesh quality parameters, such as non-orthogonality, skewness and cell volume, as well as
the influence of these parameters on the stability and accuracy of the numerical solution are carried out. For verification, the RANS (
Evaluation of the main quality parameters (non-orthogonality, skewness, cell volume) showed that the structured grid constructed using the improved block connection scheme provides better orthogonality
and skewness indices compared to the unstructured grid, which has a positive effect on the accuracy and stability of numerical simulation. The results of numerical simulation using various turbulence
models (
The obtained results allow us to conclude that it is appropriate to choose a grid generation method depending on the features of the problem geometry and the turbulence models used. The work is of interest to specialists in the field of computational fluid dynamics and engineers using OpenFOAM to model flows in complex pipeline systems.