ISSN 2658–5782
DOI 10.21662
Electronic Scientific Journal


© Институт механики
им. Р.Р. Мавлютова
УФИЦ РАН

Яндекс.Метрика web site traffic statistics

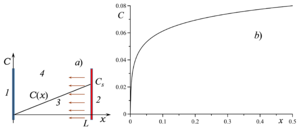
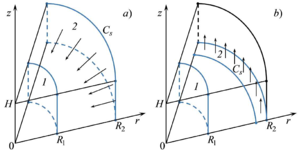
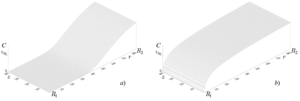
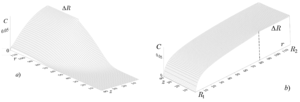
Demin V.A., Demina T.V., Zinurova V.E. Penetration of a Silicon Vapor through Residual Gaseous Medium during Siliconizing of a Carbon Composite Material. Multiphase Systems. 19 (2024) 3. 103–111 (in Russian).
2024. Vol. 19. Issue 3, Pp. 103–111
URL: http://mfs.uimech.org/mfs2024.3.015,en
DOI: 10.21662/mfs2024.3.015
Penetration of a Silicon Vapor through Residual Gaseous Medium during Siliconizing of a Carbon Composite Material
V.A. Demin∗,∗∗, T.V. Demina∗,∗∗∗, V.E. Zinurova∗,∗∗∗
∗Perm State National Research University, Perm, Russia
∗∗Perm National Research Polytechnic University, Perm, Russia
∗∗∗Institute of Continuous Media Mechanics, Perm, Russia

Abstract

A new physical and mathematical approach is proposed for the description of a silicon vapor high-temperature transfer from the melt mirror to the surface of absorbing carbon porous medium in an atmosphere of residual gas under moderate vacuum conditions. The general hydrodynamic equations are simplified as much as possible and lead to the model, which is intended for further numerical implementation in the course of simulation the non-stationary three-dimensional process of high-temperature siliconizing of porous carbon products of arbitrary shape and under the condition of complex distribution of silicon sources and sinks. The physical and mathematical model of transport consists of only one non-linear differential equation in partial derivatives for the silicon vapor concentration in the atmosphere of argon or any other residual gas. The main achievement consists of obtaining two stationary analytical solutions for plane and cylindrical geometry in one-dimensional formulation of the problem, which explain the anomalously large silicon vapor flux into the porous material in full-scale experiments. The exact solutions for the studied gas mixtures are expressed in terms of the well-known verified values of material parameters. The high degree of the model usability is supported by numerical simulation in a non-steady two-dimensional case. It has shown that despite the low saturation density of gaseous silicon, the vapor-liquid phase process of high-temperature siliconizing of the carbon material is physically possible in a reasonable time.

Keywords

high temperature processes,
rare gaseous medium,
transfer of silicon vapor,
diffusive and convective transport

The authors acknowledge financial support by the Ministry of Science and Higher Education of the Russian Federation (theme №124021600038-9)

References

  1. Narottam P. Ceramic Matrix Composites Materials, Modeling and Technology. Bansal P. and Lamon Jacques (Eds). Chromatographia, 2015, 78, 843– 844.
    DOI: 10.1007/s10337-015-2883-1
  2. Shang J. Durability Testing of Composite Aerospace Materials Based on a New Polymer Carbon Fiber-Reinforced Epoxy Resin. Fluid Dynamics and Material Processing, 2023, 19(9), 2315–2327.
    DOI: 10.32604/fdmp.2023.026742.
  3. Shikunov, S.L., Kurlov, V.N. SiC-based composite materials obtained by siliconizing carbon matrices. J. Technical Physics, 2017, 62(12), 1869–1876.
    DOI: 10.1134/S1063784127120222
  4. Kulik A.V., Kulik V.I., Ramm M.S., Demin S.E. Development of a model and numerical study of the processes for production composites with a SiC matrix by vapour-phase siliconization. Proceedings of the IV-th International Conference ”Functional nanomaterials and high-purity substances“, Moscow: Inst. of Metallurgy and Materials Science, RAS, Suzdal, Russia, 2012.
  5. Kulik A.V., Kulik V.I., Ramm M.S. Demin, S.E. Numerical study of gradient CVI processes for production of SiC-matrix composites. Proceedings of V-th International Conference ”Functional nanomaterials and high-purity substances“, Moscow: Inst. of Metallurgy and Materials Science, RAS, Suzdal, Russia, 2014.
  6. Demin V.A., Maryshev B.S., Menshikov A.I. Numerical modelling of a high temperature silicification process in the carbon-carbon porous medium. Bulletin of Perm University. Physics, 2021, No. 3, 56–62 (in Russian).
    DOI: 10.17072/1994-3598-2021-3-56-62
  7. Menshikov A.I. Theoretical modeling of the processes of condensation and adsorption during the saturation of porous materials (Ph.D. Thesis) Perm State National Research University. Russia. 2022.
  8. Stull D.R. Vapor pressure of pure substances. Ind. and Eng. Chem., 1947, 39(4), 517–550.
    DOI: 10.1021/ie50448a022
  9. Tomooka T., Shoji Y., Matsui T. High Temperature Vapor Pressure of Si. J. Mass Spectrom. Soc. Jpn., 1999, 47 (1), 49–53.
    DOI: 10.5702/massspec.47.49
  10. Hirschfelder J.O., Curtiss Ch.F., Bird R.B. Molecular theory of gases and liquids. New York: Wiley and Sons, 1954, 1–1219.
    DOI: 10.1063/1.3061949
  11. Landau L.D., Lifshitz E.M. Fluid Mechanics. Course of Theoretical Physics. Oxford: England: Pergamon Press, Ltd., 1966, 6, 1–536.
  12. Nield D.A., Bejan A. Convection in porous media. New York: Springer, 2006, 1–654.
    DOI: 10.1007/978-3-319-49562-0
  13. Demin, V.A., Petukhov, M.I., Ponomarev, R.S., Topova, A.V. On a role of anisotropy and nonlinear diffusive effects during the construction of waveguides in the lithium niobate. Bulletin of Perm University. Physics, 2021, 1, 49–58 (in Russian).
    DOI: 10.17072/1994-3598-2021-1-49-58
  14. Vohra, S.T., Mickelson, A.R., Asher, S.E. Diffusion characteristics and waveguiding properties of proton exchanged and annealed LiNbO3 channel waveguides. J. of Applied Physics(AIP), 1989, 66(11), 5161–5174
    DOI: 10.1063/1.343751
  15. Korn G.A., Korn T.M. Mathematical handbook for scientists and engineers. McGraw-Hill Book Company, 1968, 1-831.
    DOI: 10.1002/zamm.19690490921
  16. Samarskii, A.A. The theory of difference schemes. New York: Marcel Dekker, Inc., 2001, 1–762.
    DOI: 10.1201/9780203908518