Islamov A.I., Nabiullina K.R. Modeling of temperature convection in microtubes under point heating:
dependence of convection velocity on tilt angle. Multiphase Systems. 19 (2024) 3. 94–102 (in Russian).
Modeling of temperature convection in microtubes under point heating: dependence of convection velocity on tilt angle
A.I. Islamov, K.R. Nabiullina
Ufa University of Science and Technology, Ufa, Russia
Abstract
This paper presents the results of a study of the dependence of the convection velocity of a liquid in a microtube on the angle of inclination
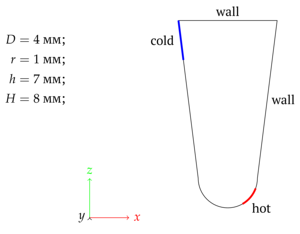
during point heating. This study utilizes a previously prepared finite-volume mesh of a cone-shaped microtube for use within the OpenFOAM
software package. A detailed analysis and description of the mathematical model and a series of computational experiments using the
built-in buoyantBoussinesqPimpleFoam solver are performed.
An important step in this paper is the post-processing of the results obtained from a series of computational experiments. The
paper provides a detailed description of the features of the data processing carried out for direct quantitative comparison of the results
obtained in the individual experiments of the series.
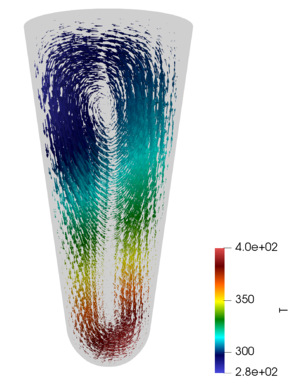
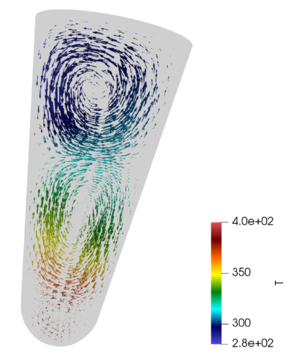
In the conducted computational experiments, quantitative data were obtained to reveal the dependence of the liquid convection
velocity in a microtube on the angle of inclination during spot heating. From the obtained results, a significant influence of the inclination
angle on the convection velocity was revealed, which can serve as a solution for the problems of optimization of mixing processes in
microscale systems in the future.
KeywordsPCR,
polymerase chain reaction,
OpenFOAM,
temperature convection,
Boussinesq approximation
Article outline
This work is part of a more general problem related to the issue of PCR (polymerase-chain reactions) acceleration. These reactions are used to multiply trace amounts of DNA molecules to volumes sufficient for analysis (sequencing). With standard approaches, PCR takes tens of minutes to hours, which is unsatisfactory for mass studies or rapid testing. There are experimental works showing that by organizing thermoconvection, PCR time can be reduced to a few minutes.
The main objective of this study was to perform mass computational experiments and analyze the results obtained using the model, method and computational grid obtained previously. To achieve this goal, the following objectives were set: based on the built-in solver buoyantBoussinesqPimpleFoam, to conduct a series of computational experiments at different tilt angles of the test tube α∈[-90;90]; to implement the mechanism for quantifying temperature convection with post-processing of data in the Python programming language; to analyze the obtained data and reveal the dependence of the convection velocity of the liquid in the microtube on the tilt angle during point heating; to determine the optimal tilt angle at which the highest convection velocity is achieved.
This study utilizes a previously prepared finite-volume mesh of a cone-shaped microtube for use within the OpenFOAM software package. A detailed analysis and description of the mathematical model and a series of computational experiments using the buoyantBoussinesqPimpleFoam built-in solver are performed. This paper also provides a detailed description of the features of the data processing carried out to directly quantitatively compare the results obtained in the individual experiments of the series.
In the computational experiments conducted, quantitative data were obtained to reveal the dependence of the convection velocity of liquid in a microtube on the angle of inclination during spot heating. From the results obtained, a significant influence of the tilt angle on the convection velocity was revealed, which can further serve as a solution for the problems of optimization of mixing processes in microscale systems.
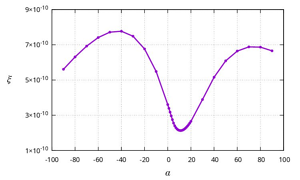
From the results presented in this paper, it was found that the maximum estimate of thermal convection velocity is achieved at a tilt angle of α = – 40°, at a tilt angle of α = – 11° the lowest estimate of thermal convection velocity is observed, also at tilt angles of α = – 90° and α = 90° a decrease in convection velocity is noticed.
In addition to the estimation of convection velocity at different angles of inclination, the obtained calculations allow us to obtain a volumetric field of velocities (for any component of the velocity vector), temperatures, and pressure, on the basis of which we can continue studies with the inclusion of additional chemical reactions, including temperature-dependent ones, to analyze the production of DNA strands. It should be clarified that the rate of thermal convection is not the only important factor in accelerating PCR assays. In addition to this assessment, other factors should be considered, such as maintaining a certain temperature at a given time interval.
References
- Игнатов К.Б., Мирошников А.И., Крамаров В.М. Новый подход к увеличению специфичности ПЦР // Биоорган. химия. 2003. Т. 29, № 4. С. 403–407.
EDN: ookiiz
Ignatov K.B., Miroshnikov A.I., Kramarov V.M. A New Approach to Enhanced PCR Specificity // Russian Journal of Bioorganic Chemistry. 2003. V. 29,
No. 4. Pp. 368–371.
DOI: 10.1023/A:1024953302170
- Northrup M.A., Mariella, Jr. R.P., Carrano A.V., Balch J.W. Silicon-based sleeve devices for chemical reactions. US Patent No. 5, 589, 136. Dec. 31, 1996.
https://www.osti.gov/biblio/415720
- Garafutdinov R.R., Chemeris D.A., Sakhabutdinova A.R., Moiseev K.V., Urmancheev S.F., Mikhaylenko C.I., Privalov L.Yu., Chemeris A.V. Convective
polymerase chain reaction in standard microtubes // Analytical Biochemistry. 2022. V. 641. 114565.
DOI: 10.1016/j.ab.2022.114565
- Heap D.M., Herrmann M.G., Wittwer C.T. PCR amplification using electrolytic resistance for heating and temperature monitoring // Biotechniques.
2000. V. 29. P. 1006–1012.
DOI: 10.2144/00295st01
- Чернышев А.В., Мединцев С.Ф., Сочивко Д.Г., Атамасов Н.В. Исследование рабочих процессов в амплификаторе ДНК в целях повышения выхода
количества продукта полимеразной цепной реакции // Вестник МГТУ им. Н.Э.Баумана. Серия «Машиностроение». 2011. № S. С. 138–149.
Chernyshev A.V., Medintsev S.F., Sochivko D.G., Atamasov N.V. Study of working processes in dna amplifier for increasing the yield of polymerase chain
reaction product // Herald of the Bauman Moscow State Technical University. Series Mechanical Engineering. 2011. No. S. Pp. 138–149. (in Russian)
EDN: oifzql
- Bennett W.J., Richards J.B., Milanovich F.P. Convectively driven thermal-cycling. US Patent No. 6, 586, 233 B2. Jul. 1, 2003.
https://www.osti.gov/biblio/1174383
- Krishnan M., Ugaz V.M., Burns M.A. PCR in a Rayleigh-Benard convection cell // Science. 2002. V. 298. 793.
DOI: 10.1126/science.298.5594.793
- Krishnan M., Agrawal N., Burns M.A., Ugaz V.M. Reactions and fluidics in miniaturized natural convection systems // Anal. Chem. 2004. V. 76. P. 6254–
6265.
DOI: 10.1021/ac049323u
- Braun D., Goddard N.L., Libchaber A. Exponential DNA replication by laminar convection // Phys. Rev. Lett. 2003. V. 91. P. 158103.
DOI: 10.1103/PhysRevLett.91.158103
- Normand C., Pomeau Y. Convective instability: A physicist’s approach // Rev. Mod. Phys. 1977. V. 49, No. 3. P. 581–624.
DOI: 10.1103/RevModPhys.49.581
- Cook W. A proposal for warming rooms by the steam of boiling water conveyed in pipes along the walls: and a method of preventing ships from
leaking, whose bottoms are eaten by the worms // Philosophical Transactions of the Royal Society of London. 1745. V. 43, No. 476. P. 370–372.
DOI: 10.1098/rstl.1744.0079
- Lord Rayleigh O.M. F.R.S. On convection current in horizontal layer of fluid, when the higher temperature is on the under side // Philosophical
Magazine. 1916. V. 32, No. 192. P. 529–546.
DOI: 10.1080/14786441608635602
- Jeffreys H. The stability of a layer of fluid heated below // Philosophical Magazine. 1926. V. 2. P. 833–844.
DOI: 10.1080/14786442608564114
- Schmidt R.J., Milverton S.W. On the instability of a fluid when heated from below // Proceedings of the Royal Society of London. Series A, Mathematical
and Physical Sciences. 1935. V. 152, No. 877. P. 586–594.
DOI: 10.1098/rspa.1935.0209
- Eds. J.B. Edel, A.J. de Mello. Nanofluidics. Nanoscience and Nanotechnology. Cambridge: Thomas Graham House, 2009. 198 p.
DOI: 10.1039/9781847558909
- Squires Т., Quake S. Microfluidics: Fluid physics at the nanoliter scale // Revs Mod. Phys. 2005. No. 77. P. 977–1007.
DOI: 10.1103/RevModPhys.77.977
- Northrup M.A., Ching M.T., White R.M., Watson R.T. DNA amplification in a microfabricated reaction chamber // 7 Int. Conf. on Solid State Sensors and
Actuators ”Transducers’93“. 1993. P. 924–927.
- Jacobson S.C., Hergenroder R., Koutny L.B., Ramsey J.M. Open channel electrochromatography on a microchip // Analytical Chemistry. 1994. V. 66,
No. 14. P. 2369–2373.
DOI: 10.1021/ac00086a024
- Zhang C, Xing D. Miniaturized PCR Chips for Nucleic Acid Amplification and Analysis: Latest Advances and Future Trends // Nucl. Acids Res. 2007. V. 35,
No. 13. P. 4223–4237.
DOI: 10.1093/nar/gkm389
- Erill I., Campoy S., Rus J., Fonseca L., Ivorra A. Development of a CMOS-compatible PCR chip: comparison of design and system strategies // J.
Micromech. Microeng., 2004, v. 14, p. 1558—1568
DOI: 10.1088/0960-1317/14/11/018
- Matsubara Y., Kerman K., Kobayashi M., Yamanura S., Morita Y, Tamiya E. Microchamber array based DNA quantification and specific sequence detection
from a single copy via PCR in nanoliter volumes // Biosens. Bioelectron. 2005. V. 20, No. 8. P. 1482–1490.
DOI: 10.1016/j.bios.2004.07.002
- Gershuni G.Z., Luybimov D.V. Thermal vibrational convection. John Wiley and Sons, 1998. 358 p.
- Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. М.: Наука, 1972. 392 с.
Gershuni G.Z., Zhukhovitskij E.M. [Convective stability of incompressible fluid] Konvektivnaja ustojchivist’ neszhimaemoj zhidkosti. Moscow: Nauka.
1972. 392 P. (in Russian)
- Boussinesq J. Theorie de l’ecoulement tourbillonnant et tumultueux des liquides dans les lits rectilignes a grande section. Vol. 1. Gauthier-Villars.
1897. 64 p.
- Mollendorf J.C., Jann K.H. Onset of Convection in a Horizontal Layer of Cold Water // J. Heat Transfer. 1983. V. 105, No. 3. Pp. 460–465.
DOI: 10.1115/1.3245607
- Гебхарт Б., Джалурия Й., Махаджан Р., Саммакия Б. Свободноконвективные течения, тепло- и массообмен. Кн. 1, 2. М.: Мир, 1991. 1208 с.
Gebhart B., Jaluria Y., Mahajan R. L., Sammakia B. Buoyancy-induced flows and transport. Washington, DC: Hemisphere Publ. Corp., 1988. 1001 p.
https://api.semanticscholar.org/CorpusID:128746069
- Бекежанова В.Б. Исследование устойчивости равновесного состояния в модели конвекции с нелинейной зависимостью плотности от
температуры и давления // ПМТФ. 2007. Т. 48, № 2. С. 66–74.
EDN: onmexd
Bekezhanova V.B. Stability of the equilibrium state in a convection model with nonlinear temperature and pressure dependences of density //
Journal of Applied Mechanics and Technical Physics. 2007. V. 48, No. 2. Pp. 200–207
DOI: 10.1007/s10808-007-0026-7
- Славинский М.П. Физико-химические свойства элементов. М.: Металлургиздат, 1952. 765 с.
Slavinskij M.P. [Physicochemical properties of elements] Fiziko-Himicheskie svojstva elementov. Moscow: Metallurgizdat. 1952. 756 P. (in Russian)
- Кулешов В.С., Моисеев К.В., Урманчеев С.Ф. Изолированные режимы течений при конвекции аномально термовязкой жидкости в плоской
ячейке // Прикладная математика и механика. 2019. № 3. С. 484–494.
DOI: 10.1134/S0032823519030093
Kuleshov V.S., Moiseev K.V., Urmancheev S.F. Isolated Convection Modes for the Anomalous Thermoviscous Liquid in a Plane Cell // SpringerLink.
2019. № 54. С. 983–990.
DOI: 10.1134/S0015462819070097
- Кулешов В.С., Моисеев К.В. Конвекция термовязкой жидкости в ячейке, подогреваемой сбоку // Многофазные системы. 2019. T. 14, № 1. С. 67–72.
Kuleshov V.S., Moiseev K.V. Convection of thermoviscouse fluid in a cell heated from the side. Multiphase Systems. 14 (2019) 1. 67–72 (in Russian).
DOI: 10.21662/mfs2019.1.010
- Кулешов В.С. Стационарные режимы конвекции жидкости с гауссовской зависимостью вязкости от температуры // Труды Института механики
им. Р.Р. Мавлютова Уфимского научного центра РАН. 2016. Т. 11, № 2. С. 218–225.
Kuleshov V.S. Stationary fluid convection modes with a Gaussian viscosity dependence of temterature Proceedings of the Mavlyutov Institute of
Mechanics. 2016. 11(2). 218–225. (in Russian)
DOI: 10.21662/uim2016.2.032
- OPENFOAM®
https://openfoam.org/ (дата обращения 10.04.2024)
- Open MPI: Open Source High Performance Computing
https://www.open-mpi.org/ (дата обращения 10.04.2024).