Article outline

In the framework of solving the problem of acoustic wave scattering on a set of small spherical obstacles, one of the most important subtasks is to determine the main characteristic of the scattering phenomenon, namely, the total scattering cross section. When waves fall on many sound-permeable obstacles, some of them, cut by each of these obstacles, are scattered repeatedly on other obstacles (additional sound fields are formed), and part of the waves pass through their boundaries. The study of the total scattering cross section, which takes into account multiple scattering, for systems of sound-permeable spheres when a wave is incident from an external source is an urgent task. Its solution will make it possible to establish at what parameters of the system the interaction between particles is insignificant and can be neglected (in this case, the problem can be simplified and reduced to the case of many single particles), and at what parameters this interaction cannot be neglected.

The main purpose of this work is to determine the ratios of the physical parameters of the sphere and the environment for given types of system configuration, in which the effects of multiple scattering are significant.

Research methods. The problem is solved numerically using a generalized calculation technique based on the fast multipole method, which allows achieving high accuracy of the results obtained with minimal CPU time. The total scattering cross section for a set of sound-permeable spheres is determined by an explicit formula obtained by the author in a previous work. This formula is applicable for any number of spheres of different radii arbitrarily located in three-dimensional space, as well as for arbitrary external influence.

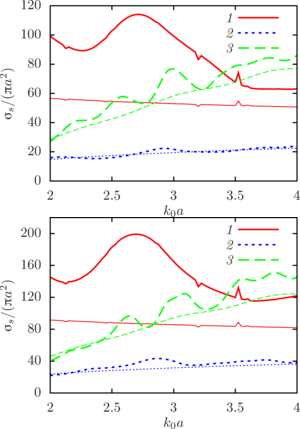
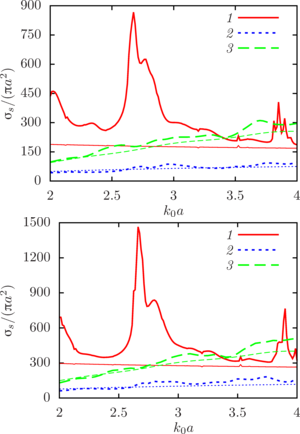
The main findings. To determine the ratios of the physical parameters of the sphere and the environment, under which the effects of multiple scattering are significant for given types of system configuration, a series of computational experiments was carried out to calculate the main scattering characteristic taking into account multiple scattering, as well as the sums of characteristics for single sound-permeable spheres. It is shown that in all the cases considered, the effects of multiple scattering cannot be neglected when determining the total scattering cross section, and

•  in the case of air bubbles in water, the type of system configuration is an essential factor;
•  for water droplets in air, both the type of configuration and the number of spheres in it are essential;
•  for dichloroethane droplets in water, the type of configuration and the number of spheres in it are insignificant factors.

Conclusion. In the case of air bubbles in water, at the considered values of the wave radius, resonances are observed that are smaller in magnitude than the monopole (“giant”) resonance, which is consistent with the known data. However, in the case of a “three-layer“ configuration, resonances of sufficiently large magnitude appear at the considered frequencies. It can be assumed that they are a consequence of multiple scattering in the volume configuration. This statement requires additional research, which is planned to be carried out in future work.