ISSN 2658–5782
DOI 10.21662
DOI 10.21662
Electronic Scientific Journal
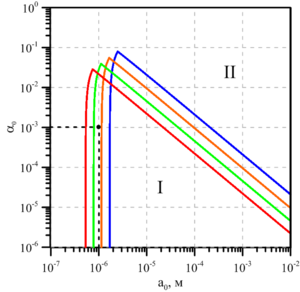
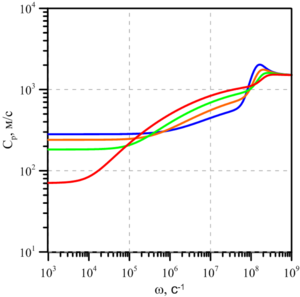
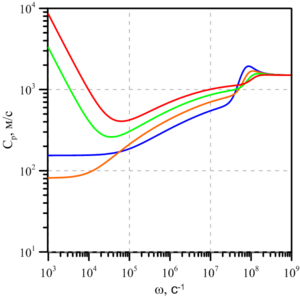
It is known that the physicochemical properties of liquids in a metastable state are mainly determined by the presence of various inclusions in their composition, for example, gas bubbles or solid particles, and it has been established that, under mechanical and thermal equilibrium, the state of a liquid with gas bubbles distributed over the volume due to the action of capillary forces at the interface, always overheated. In this paper, we consider the propagation of weak perturbations in a superheated water-air bubbly medium, when, in addition to water vapor, the bubbles contain an inert gas (for example, air) that does not participate in phase transitions. To describe the problems under consideration, a system of equations is used, which consists of the laws of conservation of mass, the number of bubbles, momentum equations, the Rayleigh–Lamb equation, the equation of heat conduction and diffusion. The solution is sought in the form of a damped traveling wave. Based on the solution of the dispersion equation, maps of the stability zones of the systems under consideration were constructed depending on the magnitude of the liquid overheating on the plane ”volume content — bubble radius“.
superheated liquid,
bubbles,
phase transition,
harmonic waves,
phase velocity,
damping factor
Purpose: Study of the characteristics of an acoustic wave in a bubbly liquid depending on the parameters of the medium.
Solution Methods: In this work, an analytical solution of the system is used. To obtain the characteristics of the wave, the wave number and the volume content of bubbles are numerically calculated depending on the initial data.
The result of the study:
On the basis of analytical and numerical calculations, a map of the stability zones of a bubbly vapor-gas-liquid mixture was constructed depending on the initial pressure in the mixture. It has been established that an increase in the initial pressure of the mixture shifts the stability zone to the left and down, which indicates an expansion of the stability zone.
It is shown that for mixture parameters that do not correspond to the stability zone, the phase velocity has the form of a nonmonotonic function in the low-frequency region.
