Многофазные системы

Fattakhov S.R. Study of pressure wave dynamics in a channel with a spherical bubble cluster. Multiphase Systems. 18 (2023) 1. 27–31 (in Russian).

2023. Vol. 18. Issue 1, Pp. 27–31
URL: http://mfs.uimech.org/mfs2023.1.004
DOI: 10.21662/mfs2023.1.004

Study of pressure wave dynamics in a channel with a spherical bubble cluster

Fattakhov S.R.

Ufa University of Science and Technology, Ufa, Russia

Abstract

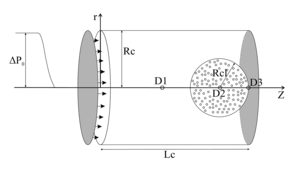
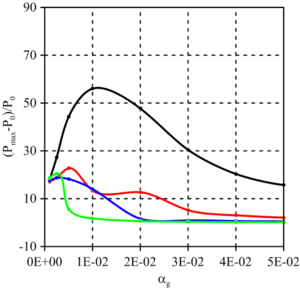
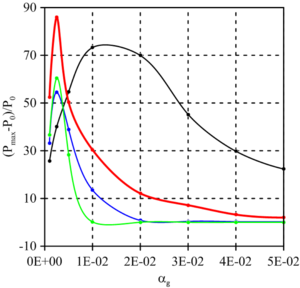
The features of wave propagation in a bubbly liquid are associated with the combined interaction of nonlinear, dispersive, and dissipative effects. In a liquid with bubbles, the properties of a practically incompressible liquid, which is a carrier phase, change dramatically with a small volume (and even more so, mass) addition of gas (bubbles), which is a dispersed phase. The peculiarity of bubbly liquids is due to their high static compressibility while maintaining a high density close to that of the liquid, which in turn leads to a low equilibrium speed of sound. In this paper, we study two-dimensional axisymmetric wave perturbations in a channel with water containing a spherical cluster filled with a water-air bubble mixture and located at one of the end boundaries. Based on the results of numerical calculations, the dependence of the maximum pressure amplitude formed in the channel on the geometrical parameters of the cluster is analyzed. It has been established that the presence of a near-end bubble cluster can significantly both increase and decrease the effect of the wave signal incident on the wall, depending on the size of the cluster and its characteristics.

Keywords

cylindrical channel,
bubble cluster,
bubble liquid,
pressure wave,
spherical bubble cluster

Article outline

Purpose: Investigation of a pressure wave passing through a bubble spherical cluster.

Solution methods: In this work, as a numerical method for solving a system of partial differential equations, a finite-difference scheme based on the use of the Runge-Kutta method was chosen. This scheme is adapted for solving problems of gas dynamics.

The result of the study:

The dynamics of ”step“ type waves in a channel with water containing a spherical bubble cluster is investigated. Based on numerical calculations, the following regularities have been established:

at certain cluster parameters, the pressure wave focuses on the end wall of the axis of the cylindrical channel;
an increase in the radius of the cluster leads to a decrease in the amplitude of the wave in the middle of the cluster, but to an increase in the amplitude of the wave that affects the end wall of the pipe behind the cluster.

References

Nigmatulin R.I. Dynamics of Multiphase Media. New York: Hemisphere, 1991, vols. 1 and 2. P. 360 and P. 464
Kedrinskii V. K. Gidrodinamika vzryva: eksperiment i modeli [Explosion hydrodynamics: experiment and models]. Novosibirsk: Izd-vo SO RAN, 2000. (in Russian)
Galimzyanov M.N. Dynamics of a pulsed signal in a cylindrical channel with a liquid containing a spherical bubble cluster // Vestnik Bashkirskogo Universiteta. 2022. Vol. 27, No 2. Pp. 275-286 (in Russian).
DOI: 10.33184/bulletin-bsu-2022.2.5
Shagapov V.Sh., Vakhitova N.K. Waves in a bubble system in the presence of gas-phase chemical reactions // Combust Explos Shock Waves. 1989. Vol. 25. Pp. 669–677.
DOI: 10.1007/BF00758728
Galimzyanov M.N. Pressure waves in a tube filled with a liquid with a bubble region in it in the form of a torus // Multiphase Systems. 2021. Vol. 16. No. 3–4. Pp. 112–120 (in Russian).
DOI: 10.21662/mfs2021.3.015