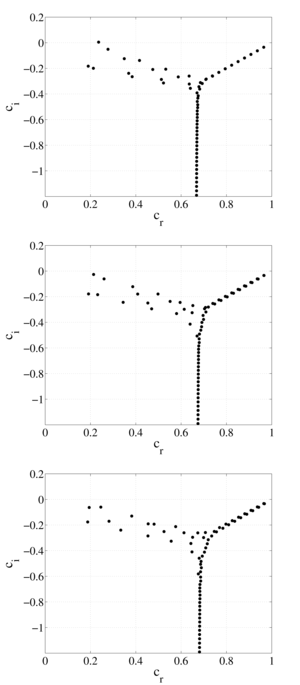
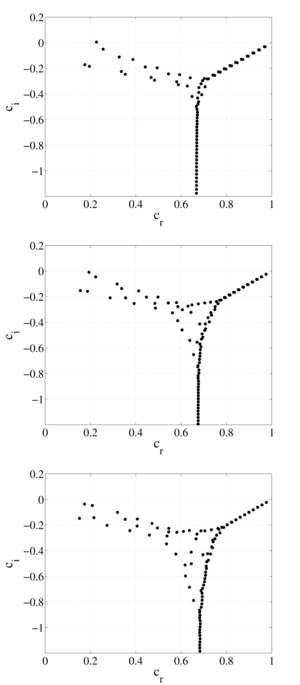
The flow of a thermoviscous model fluid in an annular channel with a given temperature field is considered. The problem of the stability of the flow of a thermoviscous fluid is solved on the basis of the generalized equation by the spectral method of expansion in Chebyshev polynomials of the first kind. The effect of taking into account the exponential dependence of the fluid viscosity on temperature and channel geometry on the spectral characteristics of the equation of hydrodynamic stability of an incompressible fluid flow in a flat channel for various wall temperatures is studied. Spectral patterns of eigenvalues of the generalized equation are constructed. The spectral characteristics determine the structure of the eigenfunctions and the critical parameters of the flow of a thermoviscous fluid. In this case, the eigenfunctions demonstrate the behavior of transverse velocity perturbations, their possible growth or decay with time. It is shown that the structure of the spectra largely depends both on the properties of the liquid, determined by the index of the functional dependence of viscosity, and on the geometry of the channel. It has been established that for small values of the thermoviscosity parameter, the spectrum is comparable to the spectrum for an isothermal fluid flow in a flat channel, however, as it increases, the number of eigenvalues and their density increase, that is, there are more points at which the problem has nonzero amplitudes of transverse velocity perturbations. The stability of a thermoviscous fluid flow depends on the presence of an eigenvalue with a positive imaginary part among the entire set of found eigenvalues for fixed parameters of the Reynolds number and wave number. It is shown that, at fixed values of the Reynolds number and wave number, the flow can become unstable with an increase in the thermoviscosity parameter.
thermoviscous liquid,
hydrodynamics instability,
spectra of eigenvalues,
annular channel
The purpose of this work is to study the hydrodynamic stability of the flow of thermoviscous liquids with a monotonic temperature dependence of viscosity and to search for parameters characterizing the flow regimes.
Solution methods. The problem of the stability of the flow of a thermoviscous fluid is solved on the basis of the generalized equation obtained earlier by the spectral method of expansion in terms of Chebyshev polynomials of the first kind.
The study found:
At present, sufficient groundwork has been accumulated in the study of the stability of fluid flows in flat channels, however, when studying this problem, the influence of the temperature factor on the change in the flow regime is often neglected. The flows of viscous liquids arise in a number of industries during the operation of various technical installations and devices, in the implementation of a number of technological processes. In such cases, the problem of identifying the features of such a flow under different regimes is important. From the point of view of energy efficiency, the laminar regime is important, on the other hand, when taking into account the efficiency of heat and mass transfer, it is turbulent. The viscosity of a fluid is an important parameter that determines the patterns of flow.
The flow of a viscous model fluid in an annular channel with a given temperature field is considered. The effect of taking into account the exponential dependence of the fluid viscosity on temperature and channel geometry on the spectral characteristics of the equation of hydrodynamic stability of an incompressible fluid flow in a flat channel for various wall temperatures is studied. At small values of the viscosity change parameter, the undisturbed flow velocity profile is similar to the Poiseuille profile, and as it increases, the maximum value of the velocity profile tends towards the heated channel wall. This phenomenon is explained by the fact that the viscosity of the liquid near the hot wall is less than the viscosity of the liquid near the cold wall, and therefore the velocity in the region of the heated wall will be greater. The problem of the stability of the flow of a thermoviscous fluid is solved on the basis of the previously obtained generalized Orr-Sommerfeld equation by the spectral method of expansion in Chebyshev polynomials of the first kind. Spectral patterns of eigenvalues of the generalized equation are constructed. The spectral characteristics determine the structure of the eigenfunctions and the critical parameters of the flow of a thermoviscous fluid. In this case, the eigenfunctions demonstrate the behavior of transverse velocity perturbations, their possible growth or decay with time. It is shown that the structure of the spectra largely depends both on the properties of the liquid, determined by the index of the functional dependence of viscosity, and on the geometry of the channel. It has been established that for small values of the thermoviscosity parameter, the spectrum is comparable to the spectrum for an isothermal fluid flow, however, as it increases, the number of eigenvalues and their density increase, that is, there are more points at which the problem has a non-trivial solution. The stability of a thermoviscous fluid flow depends on the presence of an eigenvalue with a positive imaginary part among the entire set of found eigenvalues for fixed parameters of the Reynolds number and wave number. It is shown that, at fixed values of the Reynolds number and wave number, the flow can become unstable with an increase in the thermoviscosity parameter.
Conclusions. It has been established that taking into account the dependence of viscosity on temperature has a rather strong effect on the conclusions regarding hydrodynamic stability, which, of course, is important in the analysis of flow regimes in the channels of heat exchangers. For the same values of Reynolds numbers and wave numbers describing stable flow regimes, an increase in the thermoviscosity parameter can lead to the appearance of unstable regimes. It should be noted that a qualitative change in the structure of the eigenvalue spectra also occurs in this case. The spectral characteristics of the flow are an important part in the analysis of fluid flow regimes.