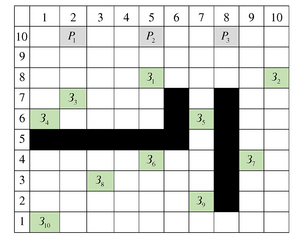
A more complex solution to the problem of the distribution of tasks in a group of mobile robots, in the presence of obstacles in the workspace, is considered. The work is a continuation of a cycle of research in which the basic algorithm for solving the tasks was one of the types of ant algorithm — the multicolonial ant system method in combination with the trajectory planning algorithm implemented using the principle of dynamic programming. The task statement, the workspace model, the goals of the robots functioning and the parameters characterizing their work have been adjusted. The choice of free parameters of the ant algorithm for performing multi-criteria optimization and tuning of the solution is carried out: the number of iterations, the number of intercolonial groups of ants, the weight of the concentration of the pheromone of arcs, the weight of the heuristic attractiveness of arcs and the pheromone evaporation coefficient. The results of computational experiments conducted in the presence of static (known in advance) and dynamic (other robots) obstacles in the workspace are presented. The proposed algorithm was tested using the example of a group consisting of three robots performing 10 tasks. As shown in the results of computational experiments, robot trajectories are built on a subset of free cells of the workspace and do not intersect cells with obstacles. At the same time, the configuration of the work field affects not only the actual routes of robots, but also the redistribution of tasks between them, and the number of robots involved. Additionally, a series of computational experiments with different combinations of values of free parameters was carried out to determine the optimal ratios and implement a more efficient ant algorithm. Optimization was carried out by a single adjustment method, which allowed us to find the required values of free parameters. It is shown that the adjustment of the parameters made it possible to reduce the relative error in the synthesis of the optimal route of movement of a group of robots by 3–6 %.
group of robots,
ant algorithm,
distribution of tasks,
trajectory planning
The solution of the problem of distribution of tasks in a group of mobile robots in the presence of various obstacles on the working field is considered. When switching to managing a group of robots, the task arises of optimally allocating the resources of the entire group, taking into account the actual list of tasks and the situation on the field of action. This task can be classified as optimizing the search for a strategy for the behavior of a group of mobile robots. The purpose of this work is to find new solutions to the problem of the distribution of tasks in a group of mobile robots, taking into account the characteristics of objects and the presence of obstacles on the working field – both static and dynamic in the form of other robots of the group. As a solution method, it is proposed to use an ant algorithm – the method of a multicolonial ant system (Ant Multi-Colony Optimization, AMCO) in combination with a trajectory planning algorithm based on the principle of dynamic programming. In earlier works of the authors, the possibility of using AMCO was already shown, but the solution of the problem was given on an empty working field, without taking into account natural obstacles. In addition, one set of parameters was selected for AMSO without analyzing its optimality.
Within the framework of the initial data, the problem statement, the workspace model, the goals of the robots' functioning and the parameters characterizing their work are formulated. The objective function is determined from the components of its main parameters:
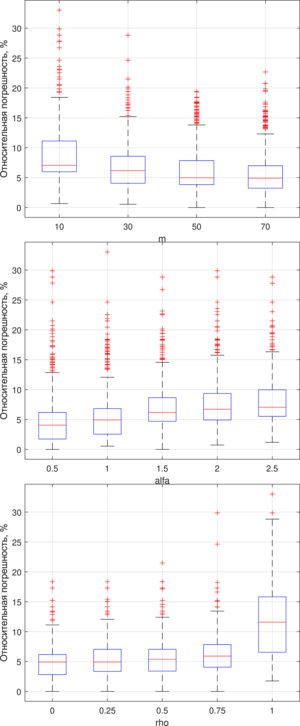
The parameters of the ant algorithm for multi-criteria optimization and tuning are selected:
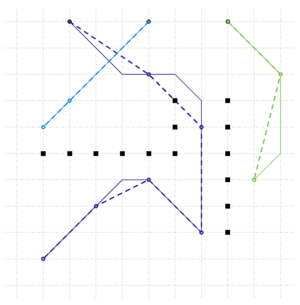
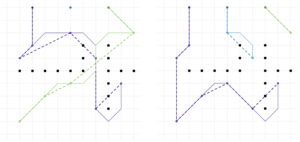
To implement the functionality of constructing motion trajectories taking into account static (obstacles on the field) and dynamic (other robots) obstacles, the trajectory planning module based on the principle of dynamic programming was used in AMSO. The simulation of the algorithm is considered on the example of a group consisting of three robots and 10 tasks. As shown in the results, the robot trajectories pass through free cells and do not cross obstacles. At the same time, the configuration of the work field affects not only the actual routes of robots, but also the redistribution of tasks between them and the number of robots involved.
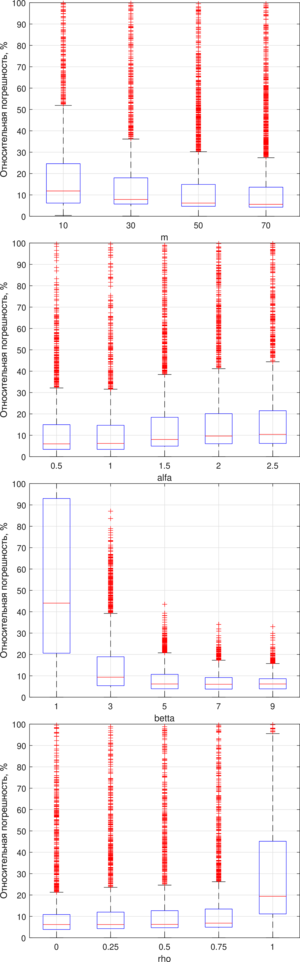
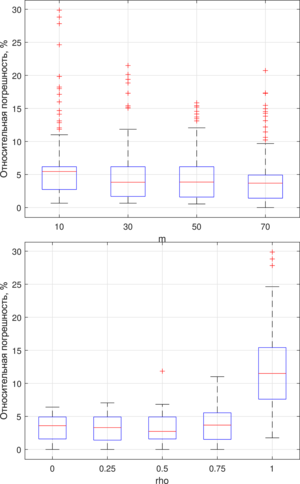
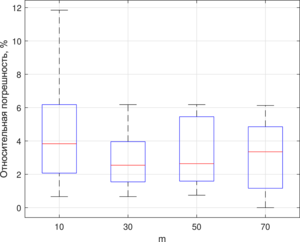
In order to establish the influence of free parameters on the effectiveness of the multicolonial ant algorithm, a series of computational experiments with different combinations of their values was carried out. The influence of the following parameters is considered:
Optimization by the method of one-time parameter adjustment made it possible to identify the following values of free AMCO parameters:
Conclusion: This article shows one of their solutions to the problems of finding the optimal management strategy for an arbitrary group of mobile robots, the complexity of which directly depends on the presence of static obstacles, dynamic obstacles in the form of other robots present in the workspace. An arbitrary number of assigned tasks, as well as a comprehensive assessment of optimality (several efficiency criteria) required the use of specific techniques and methods for modifying the previously obtained solution using an ant algorithm. The procedure for making changes to the algorithm was implemented in two stages.
At the first stage, when synthesizing the trajectories of a group of robots by introducing a new module into the AMCO algorithm that calculates the mutual movement of robots using the principle of dynamic programming, stationary (obstacles, walls) and dynamic (other robots of the group) obstacles were adequately taken into account.
The second stage consists in solving the meta-optimization problem of selecting free AMCO parameters by a single parameter adjustment method, which eventually allowed to reduce the relative error in the synthesis of optimal routes for a group of robots, and reduce total energy costs.