Многофазные системы

Nasibullaeva E.Sh. Numerical analysis of acoustic scattering from a layer of droplets under external action. Multiphase Systems. 17 (2022) 3–4. 167–176 (in Russian).

2022. Vol. 17. Issue 3–4, Pp. 167–176
URL: http://mfs.uimech.org/mfs2022.3.015
DOI: 10.21662/mfs2022.3.015

Numerical analysis of acoustic scattering from a layer of droplets under external action

Nasibullaeva E.Sh.

Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia

Abstract

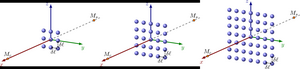
The study of acoustic scattering from small obstacles is important both for studying the fundamental nature of this phenomenon and from a practical point of view, since many applications of acoustic waves are based on the scattering phenomenon. Within the framework of the problem of acoustic scattering from a set of sound-permeable spheres arbitrarily located in space, under external influence, scattering from a layer of drops is studied. The main goal is to determine the parameters at which the system is sensitive to changes in the droplet radius. A special case of a small spheres layer is possible when a region containing many small inhomogeneities is conditionally two-dimensional one (one of the three dimensions can be neglected). The problem is solved numerically using a generalized calculation technique based on the fast multipole method, which allows achieving high accuracy of the results obtained with minimal CPU time. A series of computational experiments was carried out for various ratios of the physical parameters of the drop and the environment (density and sound speed) for a different number of spheres and the density of their arrangement in the configuration. It is shown that the system is most sensitive to changes in the droplet radius in the case when the elasticity of the substance inside the droplet is less than that of the external environment, and with an increase in the sphere number in dense configurations the system is most sensitive when the elasticity of the substance inside the droplet is much greater than that of the external environment. It is found that the sensitivity to changes in the initial data decreases with an increase in the distance between the sphere centers, that is, with a decrease in the density of the arrangement of the spheres in the configuration.

Keywords

acoustic scattering,
system of drops,
monopole radiation source,
standard deviation,
system response

Article outline

The study of the sound wave scattering phenomenon on small inhomogeneities is important both for investigating the fundamental nature of this phenomenon, and from a practical point of view, since many applications of acoustic waves are based on this phenomenon, such as sonar, sounding of the atmosphere and ocean, non-destructive testing devices, the creation of a positioned 3D sound, etc. One of the actual subtasks is to determine the pressure at some distance from the scattering layer, consisting of small sound-permeable (the wave passes through the surface) spheres (droplets), under external influence. Such subtasks may arise in cases when the region containing a set of studied inhomogeneities is conditionally two-dimensional one (one of the three dimensions of this region can be neglected).

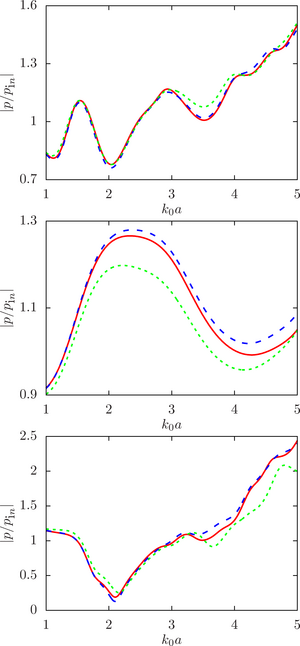
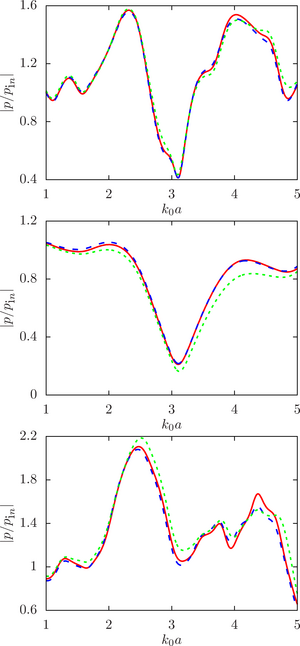
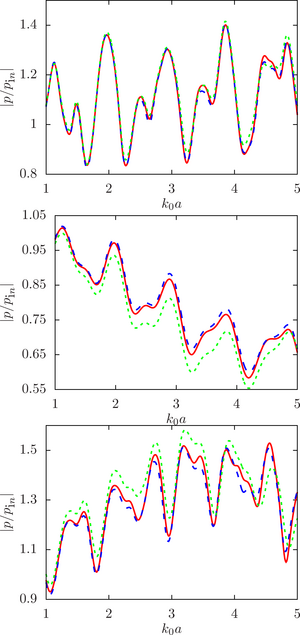
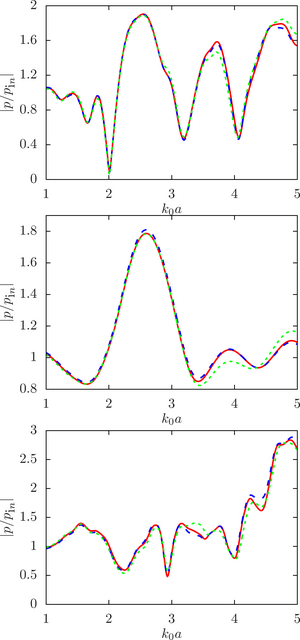
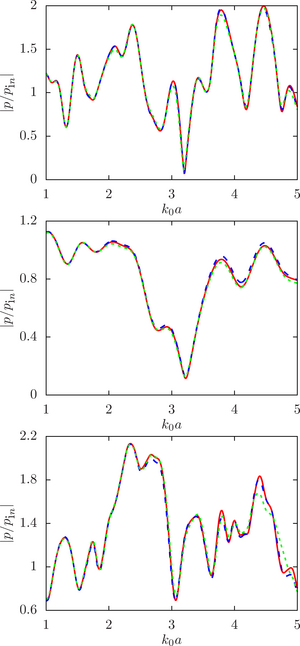
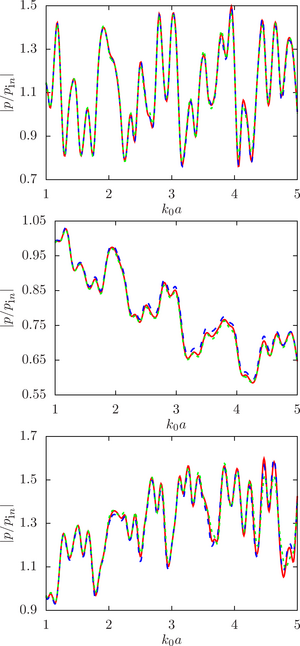
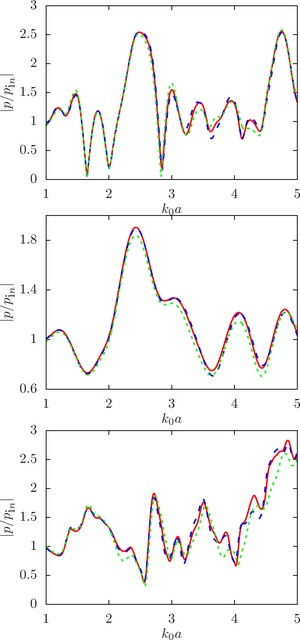
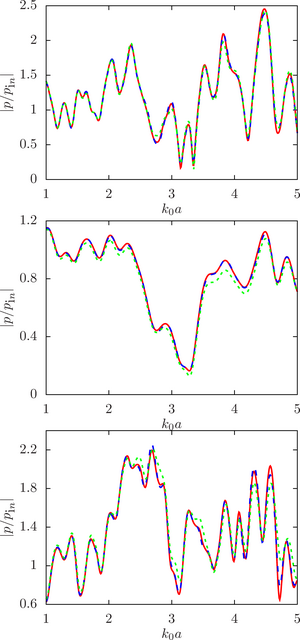
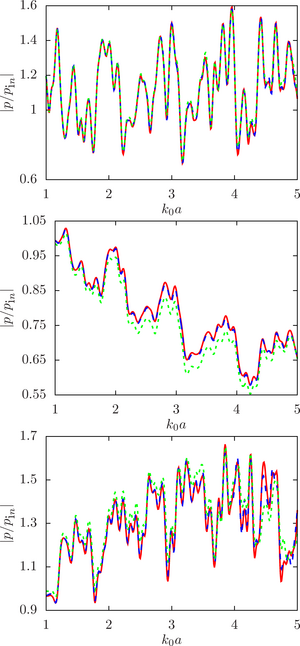
The main purpose of this work is to estimate the sensitivity of the system response to changes in the initial data, namely, the radius of the droplets, at different ratios of the physical parameters of the droplet and the environment (density and speed of sound) for a different number of spheres and the density of their location in the configuration.

Research methods. The problem is solved numerically using a generalized calculation technique based on the fast multipole method, which allows achieving high accuracy of the results obtained with minimal CPU time.

The main findings. The numerical analysis was carried out within the framework of a computational experiment in which the influence of the initial factor (the radius of the spheres) on the value of the desired function (the modulus of the normalized pressure at the calculated point) was studied. To achieve that, the drop radii were randomly set within a given deviation from the initial (undisturbed) value. A series of computational experiments was carried out for different ratios of the physical parameters of the droplet and the environment (density and speed of sound) for a different number of spheres and the density of their location in the configuration. It is shown that

the system is most sensitive to changes in the radius of droplets in the case when the ratio of the elasticity of the substance of the sphere and the external medium is less than 1;
the system becomes more sensitive to changes in the initial data in the case when the elasticity of the substance of the sphere is much greater than the elasticity of the external environment (water droplets in the air) with an increase in the number of spheres in dense configuration;
in the case when the standard deviation of the desired function is greater than the standard deviation of the radius of the spheres, the sensitivity to changes in the initial data decreases with increasing distance between the centers of the spheres;
the greater the deviation in the source data, the greater the deviation of the desired function.

Conclusion. Note that although these conclusions are based on the study of systems with a small number of spheres, it is logical to assume their validity for configurations with a large number of inclusions. However, to confirm the truth of this statement, additional research is required, which is planned to be carried out in the future.

References

Ishimaru A. Wave Propagation Scattering in Random Media, 1st Edition. New York: Academic Press, 1978. 272 p.
Stashkevich A.P. [Acoustics of the sea] Akustika morya. Leningrad: Sudostroenie, 1966. 356 p. (in Russian).
Kallistratova M.A. [Radio-acoustic sounding of the atmosphere] Radioakusticheskoe zondirovanie atmosfery. Moscow: Nauka, 1985. 197 p. (in Russian).
Technology for creating positioned 3D sound.
https://www.ixbt.com/multimedia/3dsound-tech.html (accessed: 24.10.2022).
Nasibullaeva E.Sh. [Numerical analysis of acoustic scattering from a layer of sound-permeable spheres]. Mnogofaznye sistemy [Multiphase Systems]. 2021. V. 16, No. 2. Pp. 50–57 (in Russian). DOI: 10.21662/mfs2021.2.008
Grinchenko V.T., Vovk I.V., Macypura V.T. [Basics of acoustics] Osnovy akustiki. Kiev: Naukova Dumka, 2009. 867 p. (in Russian).
Vladimirov V.S. Equations of Mathematical Physics. New York: Marcel Dekker, Inc. 1971. 426 p.
Gumerov N.A., Duraiswami R. Computation of scattering from N spheres using multipole reexpansion // J. Acoust. Soc. Am. 2002. Vol. 112, No. 6. P. 2688–2701.
DOI: 10.1121/1.1517253
Nasibullaeva E.Sh. [Numerical simulation of acoustic scattering from coaxial sound-penetrable spheres]. Mnogofaznye sistemy [Multiphase Systems]. 2019. V. 14, No. 2. Pp. 115–124 (in Russian).
DOI: 10.21662/mfs2019.2.016
Nasibullaeva E.Sh. [Numerical analysis of acoustic scattering from sound-permeable spheres under external influence]. Vestnik UGATU (scientific journal of Ufa State Aviation Technical University) [Vestnik UGATU]. 2021. V. 25, No. 2(92). Pp. 93–101 (in Russian).
DOI: 10.54708/19926502_2021_2529293[11] Nasibullaeva E.Sh. [Simulation of acoustic scattering from a set of sound-permeable spheres in 3D space]. Vychislitel’nye texnologii [Computational technologies]. 2022. V. 27, No. 2. Pp. 19–36 (in Russian).
DOI: 10.25743/ICT.2022.27.2.003
Nasibullaeva E.Sh. [Numerical analysis of multiple scattering of an acoustic wave on a set of sound-permeable spheres in 3d space]. Vychislitel’naya mexanika sploshnyx sred [Computational Continuum Mechanics]. 2022. V. 15, No. 4. Pp. 383–398 (in Russian).
DOI: 10.7242/1999-6691/2022.15.4.29
LAPACK — Linear Algebra PACKage.
https://netlib.sandia