The article is concerned with the flow of a thermoviscous fluid in a cylindrical channel for various types of viscosity functions in the joint solution of the problem of conjugate heat exchange between the channel and the surrounding material. A model of a cylindrical channel with a thermoviscous liquid flowing inside at a given velocity and viscosity is considered. The methodology of the process consists in applying a system of model equations that describes the dynamics of thermoviscous fluid flow processes based on the laws of phase energy conservation, the continuity equation, the Navier-Stokes momentum conservation equation taking into account conjugate heat transfer and the heat transfer equation for a solid. Numerical implementation of model representations was carried out using the Comsol Multiphysics digital package. Velocity and temperature profiles were obtained in the cross section of the channel. The influence of the viscosity function on the flow profile is shown, as well as the quantitative characteristics of the flow and heat transfer. An analysis was made of the dependence of the nature of the velocity and temperature profiles on the viscosity of the liquid and the type of dependence of viscosity on temperature. The result of the work done is the found features and regularities that arise in the process of conjugate heat transfer of a thermoviscous liquid in a cylindrical channel when comparing the linear and exponential dependences of viscosity on temperature. The analysis of the obtained dependences of viscosity and temperature in the flow profile, the value of the maximum flow rate was carried out. It is shown that viscous friction causes a local increase in temperature near the pipe walls, followed by an increase in fluid velocity due to a decrease in viscosity. The results obtained are basic for the further development of this topic and will be used to solve new problems in the field of modeling the thermoviscous fluid flow and conjugate heat transfer.
thermoviscous fluid, heat exchange, cylindrical channel, velocity profile,
temperature profile
The flow of thermoviscous liquids in channels plays an important role, since channels are the main nodes in heat exchange equipment. When a viscous fluid flows, its individual layers act on each other with forces that are tangential to the layers. This phenomenon is called internal friction or viscosity. Due to the symmetry of the cross section, it is clear that in the channel the particles of the flowing liquid, equidistant from the axis, have the same speed. The particles moving along the channel axis have the highest speed. In the presence of heat transfer of a thermoviscous liquid with the channel walls, the viscosity of the liquid becomes inhomogeneous, which affects the flow and heat transfer. Thus, there is a certain interest in studying the dependence of the qualitative and quantitative characteristics of thermoviscous liquid flows in channels.
The article is concerned with the flow of a thermoviscous fluid in a cylindrical channel for various types of viscosity functions in the joint solution of the problem of conjugate heat exchange between the channel and the surrounding material. A model of a cylindrical channel with a thermoviscous liquid flowing inside at a given velocity and viscosity is considered. The methodology of the process consists in applying a system of model equations that describes the dynamics of thermoviscous fluid flow processes based on the laws of phase energy conservation, the continuity equation, the Navier-Stokes momentum conservation equation taking into account conjugate heat transfer and the heat transfer equation for a solid. Numerical implementation of model representations was carried out using the Comsol Multiphysics digital package. Velocity and temperature profiles were obtained in the cross section of the channel. The influence of the viscosity function on the flow profile is shown, as well as the quantitative characteristics of the flow and heat transfer. An analysis was made of the dependence of the nature of the velocity and temperature profiles on the viscosity of the liquid and the type of dependence of viscosity on temperature. The result of the work done is the found features and regularities that arise in the process of conjugate heat transfer of a thermoviscous liquid in a cylindrical channel when comparing the linear and exponential dependences of viscosity on temperature. The analysis of the obtained dependences of viscosity and temperature in the flow profile, the value of the maximum flow rate was carried out. It is shown that viscous friction causes a local increase in temperature near the pipe walls, followed by an increase in fluid velocity due to a decrease in viscosity. The results obtained are basic for the further development of this topic and will be used to solve new problems in the field of modeling the thermoviscous fluid flow and conjugate heat transfer.
The heat transfer of a thermoviscous fluid in a cylindrical channel with a hot thermoviscous fluid flowing into the channel is simulated for various types of viscosity functions together with the solution of the problem of conjugate heat transfer of the channel with the surrounding material.
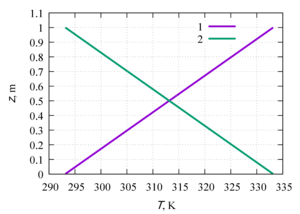
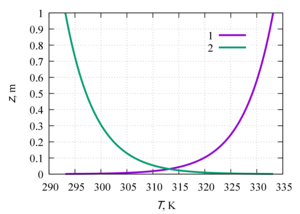
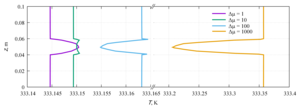
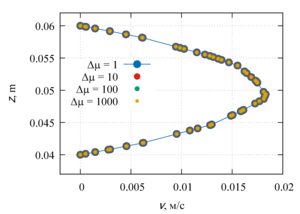
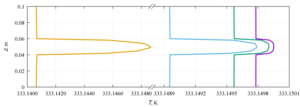
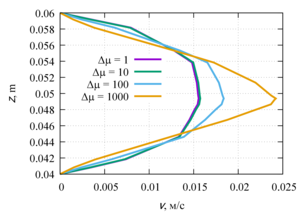
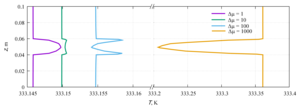
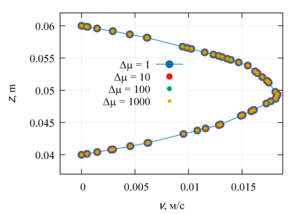
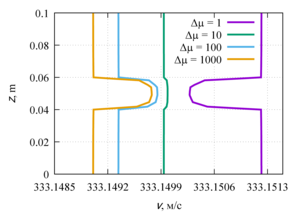
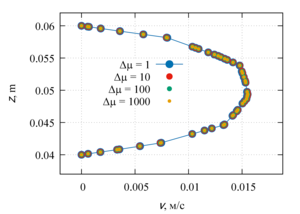
Velocity and temperature profiles were obtained along the channel axis, as well as in the central cross section of the channel. The influence of the viscosity function on the flow profile is shown, as well as the quantitative characteristics of the flow and heat transfer. Linearly and exponentially decreasing dependences of viscosity on temperature are characterized by heat transfer due to thermal conductivity. For linearly and exponentially decreasing functions, a change in the velocity profile at different Δµ was revealed, which indicates the predominance of convective heat transfer. The velocity profiles for linearly and exponentially increasing dependences of viscosity on temperature have an identical shape and the same maximum points in the channel.