Urmancheev S.F.
Dispersed media: scattering of sound waves, stratification in swirling flows and sedimentation processes. Multiphase Systems. 17 (2022) 1–2. 97–112 (in Russian).
Dispersed media: scattering of sound waves, stratification in swirling flows and sedimentation processes
Urmancheev S.F.
Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia
Abstract
A brief review on three problems from the multiphase media mechanics area related to the study of the dynamic
behavior of disperse systems under various conditions and methods of interaction with external fields or the
environment is presented. The problems are an integral part of the scientific project “Hydrodynamic effects in
multiphase and thermoviscous media under wave and thermal effects”. The review is carried out in the context of the
vector of development of modern research in the relevant areas. As a part of solving the problem of acoustic wave
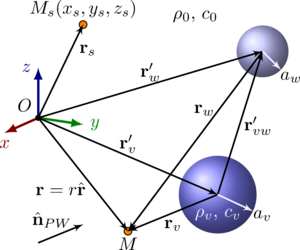
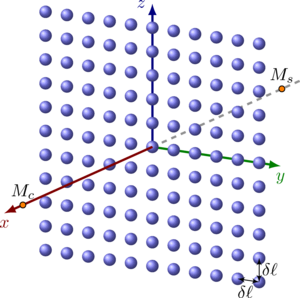
scattering by a set of spherical bubbles or drops, taking into account their sound permeability, the fast multipole
method was developed to expand the possibilities of its application in the considered cases. On the basis of addition
theorems for spherical wave functions, a new formula for the total scattering cross section for a set of interacting
sound-permeable spheres arbitrarily located in space is obtained. An important aspect of the research was the
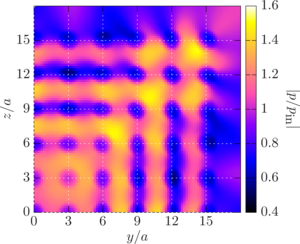
estimation of the region in the parameter space of the problem, in which the effects of multiple scattering are
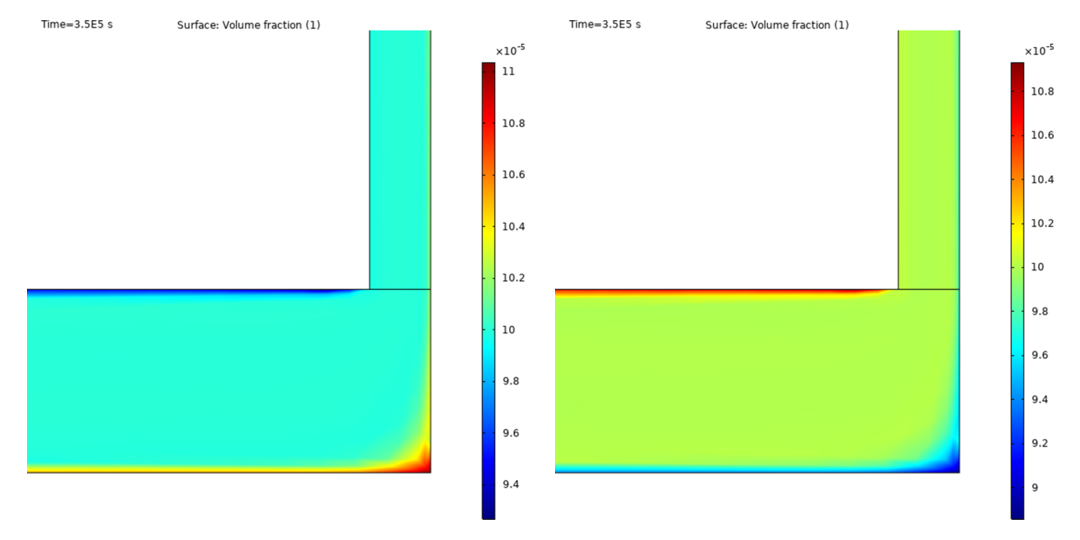
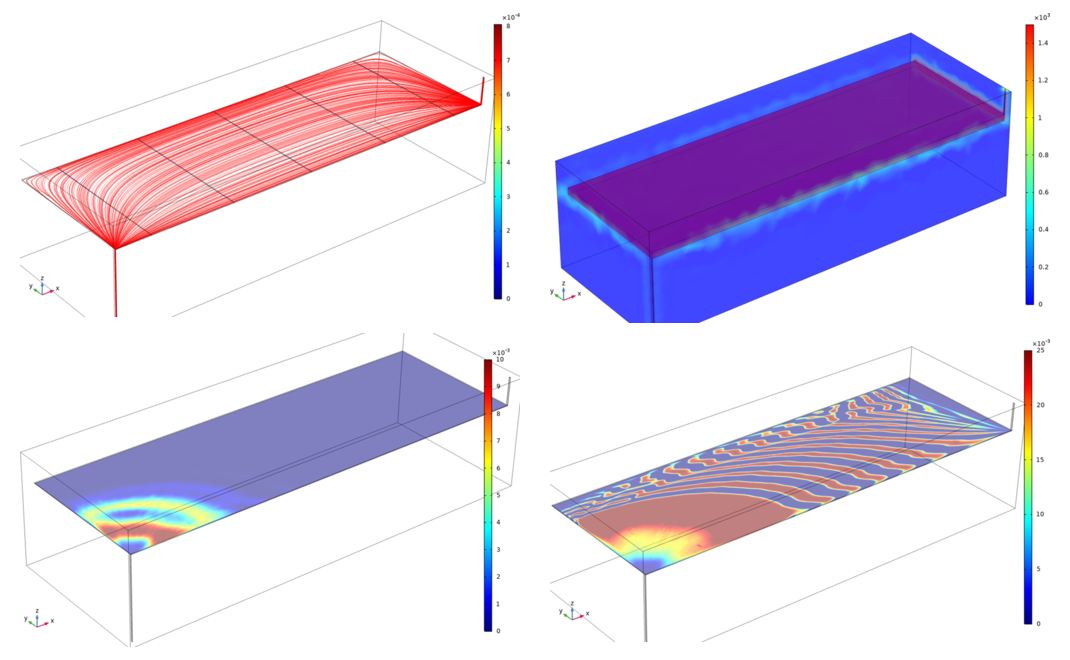
significant. The second problem is related to mathematical modeling of a swirling turbulent flow containing particles
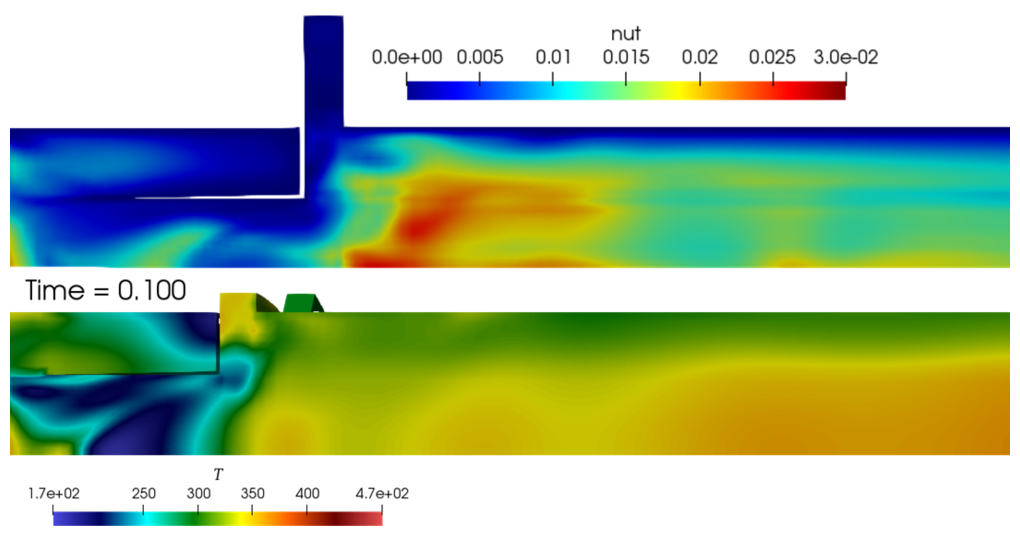
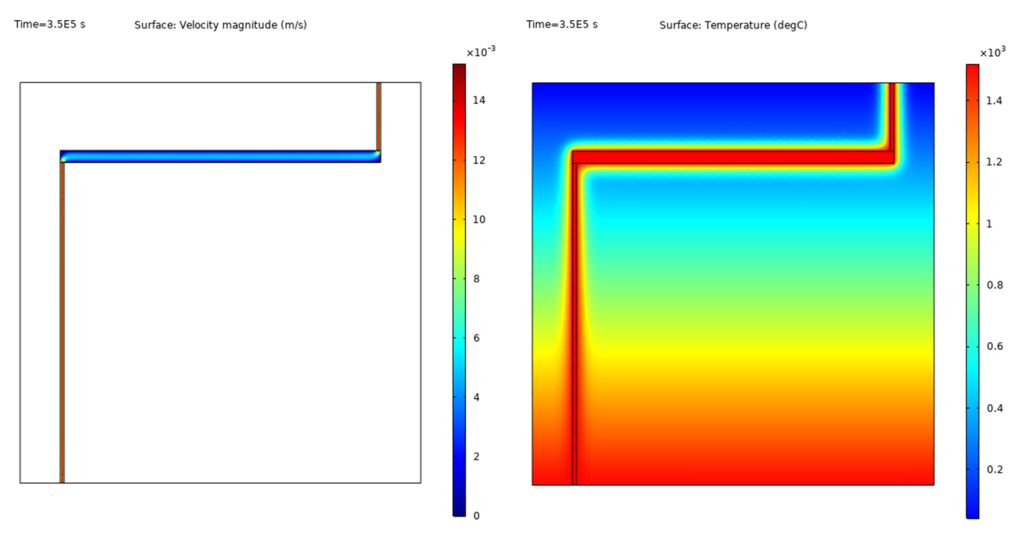
of a dispersed phase. For numerical studies of temperature stratification in a vortex tube, an algorithm and a computer
code were created using an orthogonalized finite-volume mesh with separation of the near-wall layer. A number of
parametric studies have been carried out, in particular, the dependence of the temperature of the outgoing air in
the cold diaphragm channel depending on the diameter of the diaphragm has been considered. In order to increase
the efficiency of geological exploration in solving the third problem for describing the process of magmatic ore
formation, a system of equations based on the methods of mechanics of multiphase media and thermohydrodynamics
is proposed. The mathematical model provides for the heat exchange of the magmatic melt flow with the surrounding
host rocks, as well as the release of heavy and light fractions from basaltic magma during its cooling. The results
obtained in the course of the computational experiment indicate the possibility of a periodically inhomogeneous
nature of the distribution of ore-forming fractions.
Keywordscoustic scattering,
system of sound-permeable spheres,
temperature stratification,
energy separation,
cyclostrophic adaptation,
igneous ore formation,
differentiation
Article outline
Present review presents some results for three problems carried out within the framework of the scientific project “Hydrodynamic effects in multiphase and thermoviscous media under wave and thermal effects”. The research program on this topic is connected with the establishment of fundamental laws in hydrodynamic processes occurring under the influence of temperature and acoustic fields. In the framework of the first problem, the scattering of acoustic waves on a set of interacting sound-permeable spheres is studied. The second problem is related to mathematical simulation of a swirling turbulent flow containing particles of a dispersed phase. The third problem is devoted to simulating the processes of differentiation of magmatic melts during the flow in subvolcanic chambers, taking into account heat exchange with surrounding rocks.
The purpose of the research is to determine the mutual influence of the acoustic, hydrodynamic and thermodynamic parameters of the considered systems and, at the same time, to study the patterns of distribution of particles of the dispersed phase, the physical properties of the study objects, the effects of stratification and localization.
Methods. To solve the first problem, the fast multipole method was expanded for the possibility of its application in the case of sound-permeable bubbles or drops arbitrarily located in space. In the framework of the second problem, for numerical studies of temperature stratification in a vortex tube, an algorithm and a computer code were created using an orthogonalized finite-volume mesh with separation of the near-wall layer. When solving the third problem to describe the process of magmatic ore formation, a system of equations based on the methods of mechanics of multiphase media and thermohydrodynamics was proposed. The mathematical model provides for the heat exchange of the magmatic melt flow with the surrounding host rocks, as well as the release of heavy and light fractions from basaltic magma during its cooling.
Main results. In the framework of first problem on the basis of addition theorems for spherical wave functions, a new formula for the total scattering cross section of the system under consideration was obtained. An important aspect of the research was the estimation of the region in the parameter space of the problem, in which the effects of multiple scattering are significant. When studying the second problem, a number of parametric studies were carried out. For a wide range of turbulent flows, the optimal, from the point of view of temperature stratification of the flow, geometric parameters of the inlet and outlet sections of the vortex tube were determined. The results for the third problem, obtained in the course of a computational experiment, indicate the possibility of a periodically inhomogeneous nature of the distribution of ore-forming fractions.
Conclusions.
- The results of research in solving the first problem are of interest from the point of view of identifying measurement data in acoustic diagnostics of bubble and drop systems in technological installations and for analyzing the consequences of the action of ultrasound and pressure waves on screening layers consisting of particles of the dispersed phase, if the hypotheses of the mechanics of multiphase media turn out to be inapplicable for describing the physical model of the process under consideration.
- For the second problem, the analysis of scientific literature shows that the complexity of the processes occurring in swirling flows, especially in the presence of a dispersed phase, that their description requires numerical models that could allow us to take into account with a sufficient degree of accuracy how all the design features of vortex tubes , and hydrodynamic and thermophysical features of the flow process in these pipes.
- When solving the problem of the formation of ore deposits, considered in the third problem, the methods of mathematical modeling by means of a computational experiment make it possible to improve the accuracy of predicting the localization of certain ore deposits formed during the outflow of a magmatic melt.
References
- Grinchenko V.T., Vovk I.V., Macypura V.T. [Osnovy akustiki] Basics of acoustics. Kiev: Naukova Dumka, 2009. 867 p. (in Russian).
- Gumerov N.A., Duraiswami R. Computation of scattering from N spheres using multipole reexpansion // J. Acoust. Soc. Am. 2002. V. 112, No. 6. P. 2688–2701.
DOI: 10.1121/1.1517253
- Gumerov N.A., Duraiswami R. Fast Multipole Methods for the Helmholtz Equation in Three Dimensions. Elsevier, 2004. 520 p.
DOI: 10.1016/b978-0-08-044371-3.x5000-5
- Nasibullaeva E.Sh. [Numerical simulation of acoustic scattering from coaxial sound-penetrable spheres]. Mnogofaznye sistemy [Multiphase Systems]. 2019. V. 14, No. 2. Pp. 115–124 (in Russian).
DOI: 10.21662/mfs2019.2.016
- Nasibullaeva E.Sh. [Numerical analysis of acoustic scattering from sound-permeable spheres under external influence]. Vestnik UGATU (scientific journal of Ufa State Aviation Technical University) [Vestnik UGATU]. 2021. V. 25, No. 2(92). Pp. 93–101 (in Russian).
DOI: 10.54708/19926502_2021_2529293
- Nasibullaeva E.Sh. [Simulation of acoustic scattering from a set of sound-permeable spheres in 3D space]. Vychislitel’nye texnologii [Computational technologies]. 2022. V. 27, No. 2. Pp. 19–36 (in Russian).
DOI: 10.25743/ICT.2022.27.2.003
- LAPACK — Linear Algebra PACKage.
https://netlib.sandia.gov/lapack/ (accessed: 24.10.2022).
- Nasibullaeva E.Sh. [Simulation of acoustic scattering from coaxial spheres under external action]. Certificate of state registration of the computer program No. 2020618862 (publ.: 05.08.2020) (in Russian).
eLIBRARY ID: 43889013
- Nasibullaeva E.Sh. [Terms number determination at the series truncation for the numerical solution of the problem of acoustic scattering from a sound-permeable spheres set]. Mnogofaznye sistemy [Multiphase Systems]. 2020. V. 15, No. 3–4. Pp. 176–182 (in Russian).
DOI: 10.21662/mfs2020.3.128
- Antoine X., Chniti C., Ramdani K. On the numerical approximation of high-frequency acoustic multiple scattering problems by circular cylinders // J. Comput. Phys. 2008. V. 227, No. 3. Pp. 1754–1771.
DOI: 10.1016/j.jcp.2007.09.030
- Duda R.O., Martens W.L. Range dependence of the response of a spherical head model // J. Acoust. Soc. Am. 1998. V. 104, no 5. Pp. 3048–3058.
DOI: 10.1121/1.423886
- Nasibullaeva E.Sh. [Numerical analysis of acoustic scattering from a layer of sound-permeable spheres]. Mnogofaznye sistemy [Multiphase Systems]. 2021. V. 16, No. 2. Pp. 50–57 (in Russian).
DOI: 10.21662/mfs2021.2.008
- Nasibullaeva E.Sh. [Numerical analysis of multiple scattering of an acoustic wave on a set of sound-permeable spheres in 3d space] // Vychislitel’naya mexanika sploshnyx sred [Computational Continuum Mechanics]. 2022. V. 15, No. 4. Pp. 383–398 (in Russian).
DOI: 10.7242/1999-6691/2022.15.4.29
- Ranque G.J. Experiments on expansion a vortex with Simultaneous Exhaust of hot air and cold air // Journal de Physique et Le Radium. 1933. V. 4. P. 112s–114s (in French).
- Hilsch R. The Use of the Expansion of Gases in a Centrifugal Field as Cooling Process // Review of Scientific Instruments. 1947. V. 18. P. 108–113.
DOI: 10.1063/1.1740893
- Merkulov A.P. Меркулов А.П. Vortex effect and its application in technology M.: Mashinostroenie, 1969. 182 p. (in Russian)
- Gutsol A.F. The Ranque effect // Physics-Uspekhi. 1997. V. 40, No 6. Pp. 639–658.
DOI: 10.1070/PU1997v040n06ABEH000248
- Kalashnik M.V., Visheratin K.N. Cyclostrophic adjustment in swirling gas flows and the Ranque–Hilsch vortex tube effect // J. Exp. Theor. Phys. 2008. V. 106. Pp. 819–829.
DOI: 10.1134/S1063776108040225
- Usychenko V.G. The Ranque effect as a self-organization phenomenon // Tech. Phys. 2012. V. 57. Pp. 379–385
DOI: 10.1134/S1063784212030164
- Leont’ev A.I. Temperature stratification of supersonic gas flow // Physics. Doklady. 1997. V. 42, No 6. Pp. 309–311.
eLIBRARY ID: 25515403
- Leont’ev A.I. Gas-dynamic method of energy separation of gas flows // High Temperature. 1997. V. 35, No 1. Pp. 155–157.
eLIBRARY ID: 25515598
- Leont’ev A.I. The method of temperature stratification of gas and a device for its implementation (Leont’ev’s pipe). Patent Russian Federation No 2106581.
- Leont’ev A.I. Gas-dynamic methods of temperature stratification (a review) // Fluid Dynamics. 2002. V. 37, No 4. Pp. 512–529.
DOI: 10.1023/A:1020629000437
- Burtsev S.A., Leontiev A.I. Study of the influence of dissipative effects on the temperature stratification in gas flows (Review) // High Temp. 2014. V. 52. Pp. 297–307.
DOI: 10.1134/S0018151X13060060
- Tsvetova E.V., Kovalnogov V.N., Khakhalev Yu.A.Modeling and research of the process of gas dynamic temperature s tratification to increase the efficiency of reducing natural gas // Bulletin of Ulyanovsk University. 2021. V. 10, No 2(54). Pp. 54–58.
DOI: 10.46548/21vek-2021-1054-0010
- Bashirova K.I., Mikhaylenko K.I. Three-dimensional simulation of a shock tube with OpenFOAM software Vestnik Bashkirskogo Universiteta. 2018. V. 23, No 3. Pp. 621–626.
DOI: 10.33184/bulletin-bsu-2018.3.8
- Mikhaylenko C.I. A finite volume mesh with periodic boundary conditions for a vortex tube numerical simulation // Многофазные системы. 2021. Т. 16, № 2. С. 72–78.
DOI: 10.21662/mfs2021.2.010
- Mikhaylenko K.I. Investigation of сomputational meshes for modeling the air dynamics in a vortex tube channel by OpenFOAM software. Computational Continuum Mechanics. 2022. V. 15(1). Pp. 56–66.
DOI: 10.7242/1999-6691/2022.15.1.5
- Bashirova K.I. Simulation of the sedimentation of a swirling flow of a rarefied granular medium in a cylindrical region by MP-PIC method. Multiphase Systems. 2021. V. 16(3–4). Pp. 144–148 (in Russian).
DOI: 10.21662/mfs2021.3.017
- Gazizov R.K., Lukashuk S.Yu., Mikhaylenko C.I. Development of parallel algorithms for solving problems of continuum mechanics based on the domain decomposition method [Razrabotka parallel’nyx algoritmov resheniya zadach mexaniki sploshnoj sredy na osnove principa prostranstvennoj dekompozicii] // Bulletin of UGATU. 2003. V. 4, No 1. Pp. 100–107. (in Russian)
eLIBRARY ID: 42340448
- Marin D.F., Mikhaylenko C.I., Khaziev L.Kh. The direct numerical simulation of the Ranque effect [Pryamoe chislennoe modelirovanie effecta Ranka] // Parallel numerical technology. Moscow. 2011. Pp. 539–547.
eLIBRARY ID: 22641213
- Mikhaylenko C.I. Dependence of the temperature distribution in the vortex tube on the geometry of the swirler. Proceedings of the Mavlyutov Institute of Mechanics. 2017. V. 12(2). Pp. 174–179.
DOI: 10.21662/uim2017.2.026
- Mikhaylenko C.I. Vortex tube modelling: Outlet parameter dependencies of cold air production // Journal of Physics: Conference Series. 2019. Vol. 1158, Issue 3. 032032.
DOI: 10.1088/1742-6596/1158/3/032032
- Mikhaylenko K.I., ValeevaYu.R. Highly Dispersed Medium Sedimentation from Air under Pressure Forces // Numerical Methods and Programming (Vychislitel’nye Metody i Programmirovanie). 2013. V. 14. Pp. 328–333.
eLIBRARY ID: 21014483
- Radko V.A. Model of dynamic differentiation of intrusive traps in the northwest of the Siberian Platform [Model’ dinamicheskoj differenciacii intruzivnyx trappov severo–zapada Sibirskoj platformy] // Russian Geology and Geophysics. 1991. No. 11. Pp. 19–27 (in Russian).
- Radko V.A. The facies of intrusive and effusive magmatism in the Norilsk region. St. Petersburg: Cartographic factory of VSEGEI, 2016. 226 p.
- Ilyasov A.M., Moiseev K.V., Urmancheev S.F. Numerical simulation of thermoconvection in a liquid for the case when viscosity is a quadratic function of temperature [Chislennoe modelirovanie termokonvekcii zhidkosti s kvadratichnoj zavisimost’yu vyazkosti ot temperatury] // Siberian Journal of Industrial Mathematics [Sibirskij zhurnal industrial’noj matematiki]. 2005. Vol. 8, No. 4(24). Pp. 51–59.
eLIBRARY ID: 9484545
- Kuleshov V. S., Moiseev K.V., Khizbullina S.F., Mikhaylenko K.I., Urmancheev S.F. The phenomena of convection anomalous thermoviscous fluid flow // Methamatical modelling. 2017. Т. 29. № 5. С. 16–26.
eLIBRARY ID: 29255015
- Kuleshov V. S., Moiseev K.V., Urmancheev S.F. Periodic structures during convection of an anomalously thermoviscous liquid // Bulletin of BashSU. 2017. Т. 22. № 2. С. 297–302.
eLIBRARY ID: 29729319
- Moiseev K.V., Khizbullina S.F., Bakhtizin R. N., Urmancheev S.F., Kuleshov V. S., Alferov A. V. Mathematical models of thermogravitational convection of an inhomogeneous fluid // Oil and gas business. 2017. Т. 15. № 2. С. 165–170.
eLIBRARY ID: 29931683
- Kuleshov V.S., Moiseev K.V., Urmancheev S.F. Isolated convection modes for the anomalous thermoviscous liquid in a plane cell // Fluid Dynamics. 2019. Vol. 54, No. 7. С. 983–990.
DOI: 10.1134/S0015462819070097
- Kuleshov V. S., Moiseev K. V., Urmancheev S. F. Isolated Convection Modes for the Anomalous Thermoviscous Liquid in a Plane Cell // Fluid Dynamics. 2019. Vol. 54, P. 983-–990.
DOI: 10.1134/S0015462819070097
- Kuleshov V. S.,Moiseev K.V. Convection of a thermoviscous liquid in a cell heated from the side // Multyphase systems. 2019. V. 14., No 1. Pp. 67–72.
DOI: 10.21662/mfs2019.1.010
- Moiseev K. V., Kuleshov V. S., Bakhtizin R. N. Free convective of a linear heterogeneous liquid in a square cavity at side heating // SOCAR Proceedings. 2020. №.4, P. 108–116.
DOI: 10.5510/OGP20200400472
- Titov V.V., Fedotov S.A. Mathematical modeling of the ascent of viscous magma along a vertical dike [Matematicheskoe modelirovanie pod"yoma vyazkoj magmy po vertikal’noj dajke]. Preprint IAE-3470/16. Moscow: IAE, 1981. 24 p.
- Kaddiri M., Naimi M., Raji A., Hasnaoui M. Thermal convection within a square cavity filled with non-newtonian power-law fluids and differentially heated with uniform heat fluxes // International Scientific Journal for Alternative Energy and Ecology. 2010. No. 8(88). P. 57–69.
eLIBRARY ID: 15632654
- Mikhailova-Filippova M.I., Fedotov S.A. Heat transfer of a magma flow with the walls of a fissure-dyke: a mathematical model and calculation algorithm [Teploobmen potoka magmy so stenkami treshchiny-dayki: matematicheskaya model’ i algoritm rascheta] // Journal of Volcanology and Seismology. 1994. No. 6. Pp. 17–23 (in Russian).
- Fedotov S.A., Mikhailova-Filippova M.I. Magma flow in dikes of different thickness (based on data of mathematical modeling with temperature-dependent viscosity) [Techenie magmy v dajkax raznoj moshchnosti (po dannym matematicheskogo modelirovaniya pri vyazkosti, zavisyashchej ot temperatury)] // Journal of Volcanology and Seismology. 1994. No. 6. Pp. 24–43 (in Russian).
- Mikhailova-Filippova M.I., Fedotov S.A. Magma flow through a cylindrical channel feeding a volcano: a mathematical model [Techenie magmy po tsilindricheskomu kanalu, pitayushchemu vulkan: matematicheskaya model’] // Journal of Volcanology and Seismology. 1996. No. 6. Pp. 20–30 (in Russian).
- Fedotov S.A., Mikhailova-Filippova M.I. Continuous flow of magma with decreasing flow through a cylindrical channel that feeds a volcano: conditions for long-term existence [Nepreryvnoe techenie magmy s ubyvayushchim raskhodom po tsilindricheskomu kanalu, pitayushchemu vulkan: usloviya dlitel’nogo sushchestvovaniya] // Journal of Volcanology and Seismology. 1997. No. 1. Pp. 3–16 (in Russian).
- Babeyko A.Y., Sobolev S.V., Trumbull R.B., Oncken O., Lavier L.L. Numerical models of crustal scale convection and partial melting beneath the Altiplano-Puna plateau // Earth Planet. Sci. Lett. 2002. V. 199. P. 373–388.
DOI: 10.1016/S0012-821X(02)00597-6