The paper presents an overview and examples of the use of free software for processing, analyzing and visualizing the results of computational and natural experiments. The implementation of two standard methods of approximation and data analysis is considered: the method of least squares and orthogonal central composite design. The first method allows the approximation of tabular data in the form of a polynomial of arbitrary degree. With an increase in the degree of the polynomial, the accuracy of the approximation increases, but, due to the growth of the condition number of the matrix, the correctness of the approximation decreases. It is shown that the normalization of the initial data makes it possible to increase the maximum order of the polynomial, in which there will be no loss of accuracy due to an ill-conditioned matrix. The implementation of the method in the Scilab programming language is proposed. The second method makes it possible to obtain a second-order approximation for an arbitrary number of variables, to estimate the linear and quadratic contributions of individual variables and their coupled interactions. A description of the method is presented and a scheme for constructing an extended experiment design matrix is proposed. The method is implemented in the C++ programming language, and a script written in the Scilab language is proposed to determine the error of the obtained approximation. To obtain a more accurate approximation, one can choose a function that takes into account the asymptotic features of the results of the computational experiment. An example of such an approximation is implemented in the computer algebra software wxMaxima. The presented software implementations of approximation methods additionally generate code in the Gnuplot and Scilab format, which increases efficiency for subsequent visualization or analysis of approximations. Examples of research visualization in the PGFPlots LATEX package and in the Gnuplot program using the epslatex terminal are given. Both approaches are convenient when presenting research results in the LATEX desktop publishing system.
free software,
the method of least squares,
orthogonal central composite design,
Scilab,
wxMaxima,
Latex,
Gnuplot
The paper presents an overview and examples of the use of free software for processing, analyzing and visualizing the results of computational and natural experiments. The implementation of two standard methods of approximation and data analysis is considered: the method of least squares and orthogonal central composite design.
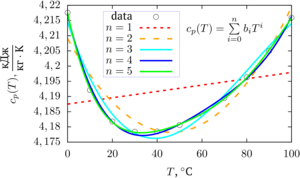
The first method allows the approximation of tabular data in the form of a polynomial of arbitrary degree. With an increase in the degree of the polynomial, the accuracy of the approximation increases, but, due to the growth of the condition number of the matrix, the correctness of the approximation decreases. It is shown that the normalization of the initial data makes it possible to increase the maximum order of the polynomial, in which there will be no loss of accuracy due to an ill-conditioned matrix. The implementation of the method in the Scilab programming language with source code generation for subsequent visualization of the approximation results using the Gnuplot sofrware is proposed.
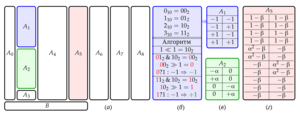
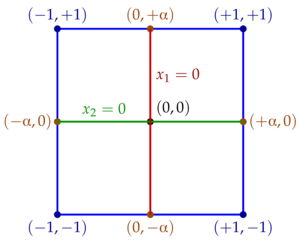
The second method makes it possible to obtain a second-order approximation for an arbitrary number of variables, to estimate the linear and quadratic contributions of individual variables and their coupled interactions. A description of the method is presented and a scheme for constructing an extended experiment design matrix is proposed. For the convenience of processing the results of the experiment, the following structure of the extended matrix was chosen: columns with a dummy parameter, a full factorial experiment, star points and a central point; coded values for coupled interactions; quadratic terms; natural values of factors and initial data (parameters and results of the experiment); the error of the objective function at the points of the design; a row containing the coefficients of the polynomial of the orthogonal central composite design. The method is implemented in the C++ programming language with the generation of the resulting polynomial in the Scilab and Gnuplot formats. To determine the error of the objective function of the obtained approximation with respect to the initial data, a script written in the Scilab language is proposed. In a rare case (when the mathematical model of the object under study completely coincides with the polynomial used), the approximation does not allow extrapolation beyond the specified range - the farther the point is outside the data range, the higher the error and the approximation becomes inadequate to the experimental or simulation data. In order to obtain a sufficiently accurate and adequate approximation, it is recommended to divide a wide range of factor values into several parts and carry out orthogonal central composite design for each of them.
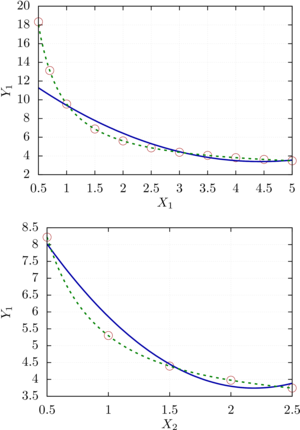
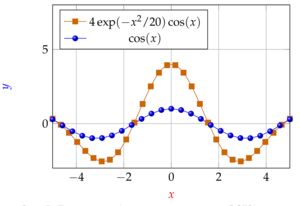
To obtain a more accurate approximation, one can choose a function that takes into account the asymptotic features of the results of the computational experiment. An example of such an approximation is implemented in the computer algebra software wxMaxima. The presented software implementations of approximation methods additionally generate code in the Gnuplot and Scilab format, which increases efficiency for subsequent visualization or analysis of approximations.
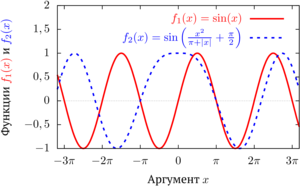
Examples of research visualization in the PGFPlots LaTeX package and in the Gnuplot program using the epslatex terminal are given. Both approaches are convenient when presenting research results in the LaTeX desktop publishing system.