Nasibullayev I.Sh.
Application of free software FreeFem++/Gmsh and FreeCAD/CalculiX for simulation of static elasticity problems.
Multiphase Systems. 15 (2020) 3–4. 183–200 (in Russian).
Application of free software FreeFem++/Gmsh and FreeCAD/CalculiX for simulation of static elasticity problems
Nasibullayev I.Sh.
Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia
Abstract
The paper discusses the stages of computer numerical simulation of engineering problems and ways to improve the
accuracy of simulation; provides a brief overview of free software for simulation elasticity problems by the finite
element method, as well as trends in the development of free CAD and CAE software. For a successful engineering
study, it is necessary to choose a convenient tool that takes into account all the features of the problem being
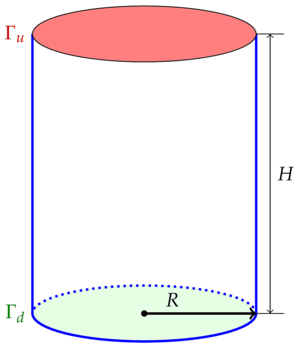
solved. Based on the solution of a test static problem of linear elasticity, two approaches to engineering modeling
were demonstrated. The first approach requires programming skills - the full modeling cycle was written in the
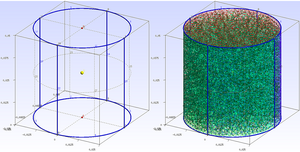
programming language of the FreeFem++ software. Additionally, the method mesh generating in the Gmsh program
with subsequent use in the FreeFem++ program is shown. In the second approach, the full cycle of modeling is
carried out through the interface of the FreeCAD program with the built-in CalculiX solver, which does not require
programming skills. A way to parameterize the task using the Python interpreter built into FreeCAD is also proposed.
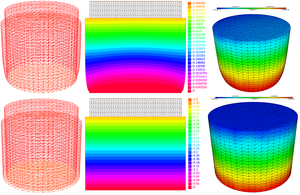
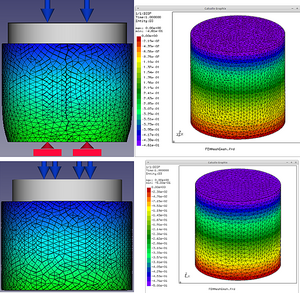
The simulation results obtained using both approaches are compared for an object to which an external action is
applied, determined by the Dirichlet or Neumann boundary conditions, and two types of object fastening are analyzed:
rigid embedding and limitation by a plane with zero friction. The analysis of the use of computing resources by
various direct and iterative methods is carried out. Within the framework of the considered test problem of static
linear elasticity, the most optimal method in FreeFem++ is the iterative method of conjugate gradients CG both in
terms of computation time and in terms of the memory used. The highest speed of calculations is provided by the
Cholesky iterative method with conditioning by the incomplete Cholesky expansion in the CalculiX program.
Keywordsstatic elasticity,
free engineering software,
FreeFem++,
Gmsh,
FreeCAD,
CalculiX,
direct and iterative solution methods of the system of linear equations
Article outline
The paper discusses the stages of computer numerical modeling of engineering problems and related programs (preprocessor, solver, and postprocessor), features of direct and iterative methods for solving of linear equations system (LES) and ways to improve the accuracy of modeling using the finite element method; provides a brief overview of free programs for modeling elasticity problems by the finite element method, as well as trends in the development of free computer-aided design and engineering analysis.
For successful engineering research, it is necessary to choose a convenient tool that takes into account all the features of the problem being solved. Based on the solution of the test static problem of linear elasticity, two approaches to engineering modeling were demonstrated. The first approach requires programming skills, and the full simulation cycle is written in the FreeFem++programming language. Additionally, the method of creating a calculated grid in the Gmsh program and then using it in the FreeFem++program is shown. In the second approach, the full simulation cycle is carried out through the interface of the FreeCAD program with the built-in CalculiX solver, no programming skills are required. A method for parameterizing the problem using the Python interpreter built into FreeCAD is also proposed. In the FreeFem++ program, the simulation was carried out using the following direct and iterative methods for solving LES: LU-decomposition, the Crout algorithm, the Cholesky decomposition; UMFPACK (Unsymmetric MultiFrontal method), the CG conjugate gradient method, and the generalized minimal residual method GMRES. The CalculiX program used a direct method for equations with sparse SPOOLS matrices and an internal iterative method with preconditioning by scaling the diagonal elements of the LES matrix ITERATIVE SCALING and with preconditioning with incomplete Cholesky decomposition ITERATIVE CHOLESKY.
The results of modeling obtained using both approaches are compared for an object to which an external influence is applied, determined by the Dirichlet or Neumann boundary conditions, and two types of fixing of the object are analyzed: rigid sealing and restriction by a plane with zero friction. The analysis of the use of computing resources by various direct and iterative methods is carried out. Iterative methods for solving LES for the problem under consideration have demonstrated a higher computational speed compared to direct methods. This is due to the fact that the three-dimensional problem was solved, and even for first-order elements, the number of equations in LES is significant. In the framework of the considered test problem of static linear elasticity, the most optimal method in FreeFem++ is the iterative method of conjugate gradients CG both in terms of calculation time and the amount of memory used. The highest calculation speed is provided by the Cholesky iterative method with the condition of incomplete Cholesky decomposition in the CalculiX program. It is shown that at the same computational cost, the accuracy of calculations for second-order elements on a coarse mesh is higher than for first-order elements on a denser mesh.
Based on the analysis of the computational capabilities of the programs, their functionality and ease of use, we will identify the features that can affect the choice of a numerical simulation program. Features of FreeFem++: programming skills are required; pre/postprocessor functions are available (creating geometry 2D/3D and generating mesh; loading a mesh created in Gmsh; visualization of calculation results); available direct methods use more computational resources compared to CalculiX; iterative methods are used with the ability to connect custom preconditioners; FreeFem++ allows you to create, rebuild, and adapt computational grids during code execution, perform full parameterization of the task, run a series of calculations based on sets of parameters, and process the results of calculations. Features of FreeCAD / CalculiX: programming skills are not required; FreeCAD / CalculiX allows you to conduct a full cycle of research within a single program, as well as parameterization of the problem in the Python programming language; as a separate program, it contains a pre/postprocessor (creating a geometry and mesh from a command file, visualizing data from a calculation results file); it has a fast and cost-effective direct SPOOLS method (compared to direct FreeFem++ methods); it has fast iterative methods with preconditioning.
References
- Ansys Mechanical — finite element analysis (FEA) software.
https://www.ansys.com/products/structures/ansys-mechanical (accessed: 22.11.2020).
- Simulia Abaqus.
https://www.3ds.com/products-services/simulia/ (accessed: 22.11.2020).
- LS-DYNA.
http://www.lstc.com/ (accessed: 22.11.2020).
- Delaunay B. Sur la sphère vide. A la mèmoire de Georges Voronoi // Bulletin de l’Académie des Sciences de l’URSS, Classe des Sciences Mathématiques et Naturelles. 1934. V. 6. P. 793–800.
http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=im&paperid=4937&option_lang=eng
- Amosov A.A., Dubinsky Yu.A., Kopchenova N.V. [Computational methods for engineers] Vychislitel’nyye metody dlya inzhenerov. M: Vysshaya shkola. 1994. P. 544 (in Russian).
- Chen K. Matrix Preconditioning Techniques and Applications, Cambridge University Press. 2005. 592 pp.
https://www.cambridge.org/core/journals/journal-of-fluid-mechanics/article/abs/matrix-preconditioning-techniques-and-applications-by-k-chen-cambridge-university-press-2005-592-pp-isbn-0521-83828-2-55/BC30A72326AF23ED5D852AD2D0B145D2
- Golub G.H., Van Loan Ch.F. Matrix Computations. Fourth Edition. The Johns Hopkins University Press. 2013. 780 pp.
- Babuška I., Szabó B.A.. Katz I.N.. The p-version of the finite element method // SIAM Journal on Numerical Analysis. 1981. V. 18. P. 515–545.
- Babuška I., Szabó B.A. On the Rates of Convergence of the Finite Element Method // International Journal for Numerical Methods in Engineering. 1982. V. 18. P. 323–341.
- Babuška I., Dorr M.R. Error estimates for the combined h- and p- versions of the finite element method // Numer. Math. 1981. V. 7. P. 257—277.
DOI: 10.1007/BF01398256
- ONELAB — Open Numerical Engineering LABoratory.
http://onelab.info/ (accessed: 22.11.2020).
- Geuzaine C., Remacle J.-F. Gmsh: a three-dimensional finite element mesh generator with built-in pre- and post-processing facilities.
International Journal for Numerical Methods in Engineering. 2009. Vol. 79, No. 11. P. 1309–1331.
http://gmsh.info/doc/preprints/gmsh_paper_preprint.pdf (accessed: 22.11.2020).
- GetDP — A General Environment for the Treatment of Discrete Problems.
http://getdp.info/ (accessed: 22.11.2020).
- FreeCAD.
https://www.freecadweb.org/ (accessed: 22.11.2020).
- Rieg F., Hackenschmidt R., Alber-Laukant B. Finite Element Analysis for Engineers. Basics and Practical Applications with Z88Aurora. Hanser. 2014. 719 pp.
- CalculiX — A Free Software Three-Dimensional Structural Finite Element Program.
http://www.calculix.de/ (accessed: 22.11.2020).
- Lyly M., Ruokolainen J., Järvinen E. ELMER - A finite element solver for multiphysics // CSC-report on scientific computing. 1999–2000. P. 156–159.
https://www.csc.fi/documents/49902/86943/cscreport.pdf (accessed: 22.11.2020).
- SALOME — the open source integration platform for numerical simulation.
https://www.salome-platform.org/ (accessed: 22.11.2020).
- Salome Meca and Code Aster.
https://www.code-aster.org/ (accessed: 22.11.2020).
- Schöberl J. NETGEN - An advancing front 2D/3D-mesh generator based on abstract rules // Computing and Visualization in Science. 1997. V. 1, No. 1. P. 41–52
DOI: 10.1007/s007910050004
- Hecht F. New development in FreeFem++ // Journal of Numerical Mathematics. 2012. V. 20, No. 3–4. Pp. 251–265.
DOI: 10.1515/jnum-2012-0013
- Nasibullayev I.Sh., Nasibullaeva E.Sh. [Fluid flow through hydraulic resistance with dynamically changing geometry] Techeniye zhidkosti cherez gidrosoprotivleniye s dinamicheski
izmenyayemoy geometriyey. Transactions of the Institute of Mechanics named after R.R. Mavlyutov, Ufa Scientific Center, Russian
Academy of Scien [Trudy Instituta mehaniki im. R.R. Mavlyutova]ces, Ufimskiy Nauchnyi Centr RAN]. 2017. V. 12, N. 1. P. 59–66 (in Russian).
DOI: 10.21662/uim2017.1.009
- Nasibullayev I.Sh., Nasibullaeva E.Sh., Darintsev O.V., [Study of fluidflow through a channel deformed by piezoelement] Izucheniye techeniya zhidkosti cherez deformiruyemyy
p’yezoelementom kanal. Multiphase Systems [Mnogofaznyye sistemy]. 2018. V. 13, No. 3. Pp. 1–10 (in Russian).
DOI: 10.21662/mfs2018.3.001
- Nasibullayev I.Sh., Nasibullaeva E.Sh., Darintsev O.V., [Simulation of fluid flow through a elastic microchannel deformed by a piezoelement in microgrip cooling systems] Modelirovaniye
techeniya zhidkosti cherez deformiruyemyy p’yezoelementom elastichnyy mikrokanal sistemy okhlazhdeniye mikrozakhvata. Mekhatronika, Avtomatizatsiya, Upravlenie. 2019. V. 20, No. 12. Pp. 740–750 (In Russian).
DOI: 10.17587/mau.20.740-750
- Chiang Ch.-Yu, Pironneau O., Sheu T., Thiriet M. Numerical Study of a 3D Eulerian Monolithic Formulation for Incompressible Fluid-Structures Systems // Fluids. 2017. V. 2, No. 2. P. 34.
DOI: 10.3390/fluids2020034
- Nasibullayev I.Sh., Darintsev O.V., Nasibullaeva E.Sh., Bogdanov D.R. Piezoelectric Micropumps for Microrobotics: Operating Modes Simulating and Analysis of the Main Parameters
of the Fluid Flow Generation // Proceedings of 15th international conference on electromechanics and robotics “Zavalishin’s reading” (Eds. by V. Shishlakov, A. Ronzhin),
Smart Innovation, Systems and Technologies, 2021. Vol. 187, Chapter 43.
DOI: 10.1007/978-981-15-5580-0_43
- Pantz O. Treatment of contact between finite deformable bodies using FreeFem++. CMAP Ecole Polytechnique. 2011
https://www.ljll.math.upmc.fr/hecht/ftp/ff++days/2011/Pantz.pdf (accessed: 22.11.2020).
- Houssein H., Garnotel S., Hecht F. Frictionless contact problem for hyperelastic materials with interior point optimizer. 2019. hal-02355429
https://hal.archives-ouvertes.fr/hal-02355429/document (accessed: 22.11.2020).
- Nasibullayev I.Sh., Darintsev O.V., [Two-dimensional dynamic model of the interaction of a fluid and a piezoelectric bending actuator in a plane channel] Dvumernaya dinamicheskaya model’
vzaimodeystviya zhidkosti i p’yezoelektricheskogo privoda s poperechnym izgibom v ploskom kanale. Multiphase Systems [Mnogofaznyye sistemy]. 2019. V. 14, No. 4. Pp. 220–232 (in Russian).
DOI: 10.21662/mfs2019.4.029
- Dhondt G. The Finite Element Method for Three-Dimensional Thermomechanical Applications. Wiley. 2004.
- Wittig K. CalculiX USER’S MANUAL — CalculiX GraphiX, Version 2.17.1. 2020.
http://www.dhondt.de/cgx_2.17.1.pdf (accessed: 22.11.2020).
- Funke A., Wittig K. An investigation of a small jet engine.
http://www.calculix.de/ (accessed: 22.11.2020).
- Abdulaziz A., Hedaya M., Mccrory J., Holford K., Elsabbagh A. Parametric Study of Honeycomb Composite Structure Using Open Source Finite Element Software. 2019.
- Vanti F., Agnolucci A., Pinelli L., Arnone A. An integrated numerical procedurefor flutter and forced response assessmentof
turbomachinery blade-rows // Proceedings of 13th European Conference on Turbomachinery Fluid dynamics and Thermodynamics ETC13, April 8-12, 2019; Lausanne, Switzerland.
- Press W.H. Numerical Recipes 3rd Edition: The Art of Scientific Computing. Cambridge University Press. 2007. P. 50–52.
- Davis T.A. Algorithm 832: UMFPACK V4.3-an unsymmetric-pattern multifrontal method // ACM Trans. Math. Softw. 2004. V. 30, No. 2. P. 196–199.
DOI: 10.1145/992200.992206
- Saad Y., Schultz M.H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems // SIAM J. Sci. Stat. Comput. 1986. V. 7. P. 856–869.
DOI: 10.1137/0907058
- Ashcraft C., Grimes R. SPOOLES: An Object-Oriented Sparse Matrix Library. PPSC. 1999.
https://static.aminer.org/pdf/PDF/000/548/747/spooles_an_object_oriented_sparse_matrix_library.pdf (accessed: 22.11.2020).
- Schwarz H.R. FORTRAN-Programme zur Methode der finiten Elemente. Teubner. 1981.
DOI: 10.1002/zamm.19830631220
- Landau L.D., Lifshitz E.M. [Theoretical physics. V. 7. Theory of Elasticity] Teoreticheskaya fizika. T. 7. Teoriya uprugosti. M.: Nauka. 2003. P. 259. (in Russian).
- Tikhonov A.N., Samarsky A.A. [Equations of mathematical physics] Uravneniya matematicheskoy fiziki. M.: Nauka. 1977. P. 735 (in Russian).
- FEM CalculiX Cantilever 3D.
https://wiki.freecadweb.org/FEM_Tutorial_Python/en (accessed: 22.11.2020).
- Zienkiewicz O.C., Taylor R.L. The finite element method. McGraw-Hill Book Company. 1989.
- FreeFEM Documentation.
https://doc.freefem.org/_static/pdf/FreeFEM-doc-v3.pdf (accessed: 22.11.2020).