Многофазные системы

Nasibullaeva E.Sh. Terms number determination at the series truncation for the numerical solution of the problem of acoustic scattering from a sound-permeable spheres set. Multiphase Systems. 15 (2020) 3–4. 176–182 (in Russian).

2020. Vol. 15. Issue 3–4, Pp. 176–182
URL: http://mfs.uimech.org/mfs2020.3.128,en
DOI: 10.21662/mfs2020.3.128

Terms number determination at the series truncation for the numerical solution of the problem of acoustic scattering from a sound-permeable spheres set

Nasibullaeva E.Sh.

Mavlyutov Institute of Mechanics UFRC RAS, Ufa, Russia

Abstract

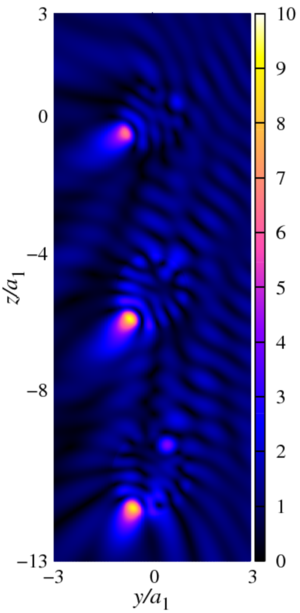
Acoustic scattering from small-sized obstacles under external influence is one of the most important problems in acoustics, primarily because of the practical applications of this phenomenon. The solution of this problem is reduced to solving the Helmholtz equation for a complex potential with certain boundary conditions. When using the calculation method based on the fast multipole method, the potentials are decomposed into series according to special spherical functions, the form of which depends on the region in which this potential is calculated. As a result, the numerical implementation of the resulting matrix system raises the question of the correct choice of the number of series members when truncating them, since with a small number of series members, the calculation accuracy will be low, and with a large one will be increase not only the accuracy, but also the calculation time. An analysis of the scientific literature has shown that there are two approaches to choosing the number of terms of a series when truncating for such problems. In the first approach, truncation of the series is based on comparing two consecutive values of the sum of the sought series until the required degree of accuracy is achieved. In the second approach, all series in each expansion are truncated for a fixed number of series terms determined using heuristic formulas. In this paper, using the example of three sound-permeable spheres of different radii in the case of their strong interaction, when numerical calculations become «sensitive» to the number of terms during truncation, we compared these approaches. The analysis of the obtained data showed that to determine the value of the desired function with the necessary accuracy, it is optimal to use a combination of the considered approaches.

Keywords

acoustic scattering,
sound-permeable spheres set,
multipole,
series truncation,
plane wave,
monopole radiation source

Article outline

Acoustic scattering from small obstacles under external influence is one of the most important problems in acoustics, primarily due to the practical applications of this phenomenon. The solution of this problem is reduced to the solution of the Helmholtz equation for a complex potential with certain boundary conditions. When applying the calculation technique based on the fast multipole method, the potentials are expanded into series in special spherical functions (multipoles), the form of which depends on the region in which this potential is calculated. As a result, in the numerical implementation of the resulting matrix system, the question arises about the correct choice of the number of terms of the series when they are truncated, since with a small number of terms in the series, the calculation accuracy will be low, and with a large number, not only the accuracy, but also the calculation time will increase.

Purpose: determination of the most optimal approach to the choice of the number of members when truncating the series for solving the problem.

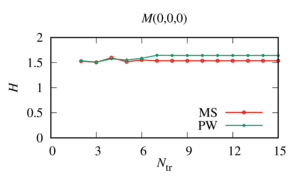
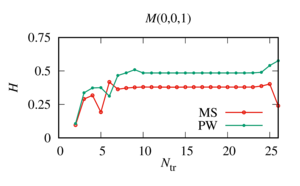
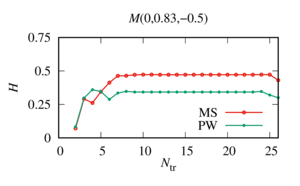
Methods: numerically analyzed the results obtained using two known approaches to truncation of series: truncation of series is based on comparing two consecutive values of the sum of the sought series until the required degree of accuracy is achieved (Approach I); all the series in each expansion are truncated for a fixed number determined using heuristic formulas (Approach II).

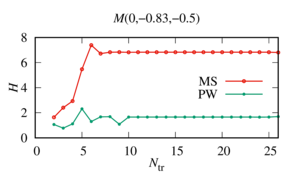
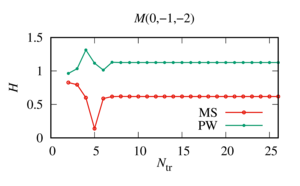
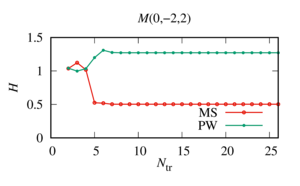
The comparison of these approaches was carried out on the example of three sound-permeable spheres of different radii in the case of their strong interaction, when numerical calculations become "sensitive“ to the number of terms upon truncation.

As a findings of the research, it has been determined that

with an increase in the distance between the spheres, the number of terms decreases when the series is truncated;
outside the spheres, the specified accuracy is achieved with a smaller value of the truncated terms in the case of small distances between the spheres;
the type of external influence (monopole source or plane wave) insignificantly affects the result;
an increase in accuracy leads to an increase in the value of the terms when the series is truncated.

Value: The analysis of the data obtained showed that to determine the number of terms when truncating the series, which makes it possible to calculate the desired function with a given accuracy, it is optimal to use a combined approach. Namely, with the help of Approach II, using heuristic formulas, the minimum value of the members of the series when truncated is determined. Then, starting at this minimum value, Approach I is applied until the required accuracy is achieved. To prevent the accumulation of errors associated with the exponential growth of the spherical Hankel functions of large order, which are included in the decomposition matrix of the system, it is necessary to control the result if the maximum value of the terms is exceeded when the series is truncated, determined by the well-known heuristic formula. In this case, the solution for the point is determined at the moment of its stabilization before the start of exponential growth, even if the specified accuracy is not achieved.

References

Nasibullaeva E.Sh. Numerical simulation of acoustic scattering from coaxial sound-penetrable spheres. // Multiphase Systems. 14 (2019) 2. 115–124 (in Russian).
DOI: 10.21662/mfs2019.2.016
Gumerov N.A., Duraiswami R. Computation of scattering from N spheres using multipole reexpansion // J. Acoust. Soc. Am. 2002. Vol. 112, No. 6. P. 2688–2701.
DOI: 10.1121/1.1517253
Duda R.O., Martens W.L. Range dependence of the response of a spherical head model // J. Acoust. Soc. Am. 1998. Vol. 104. P. 3048–3058.
DOI: 10.1121/1.423886
Antoine X., Chniti C., Ramdani K. On the numerical approximation of high-frequency acoustic multiple scattering problems by circular cylinders // J. Comput. Phys. 2008. Vol. 227, No. 3. P. 1754–1771.
DOI: 10.1016/j.jcp.2007.09.030
Chew W.C., Jin J.M., Michielssen E., Song J. Fast and Efficient Algorithms in Computational Electromagnetics. Norwood: Artech House Antennas and Propagation Library, 2001. 932 p.
Amamou M.L. A theoretical and numerical resolution of an acoustic multiple scattering problem in three-dimensional case // Acoustical Physics. 2016. Vol.62, No. 3. P. 280–291.
DOI: 10.1134/S1063771016030015