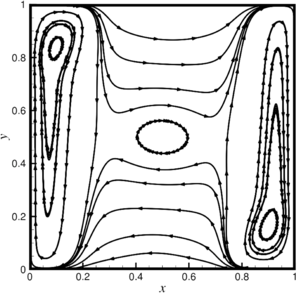
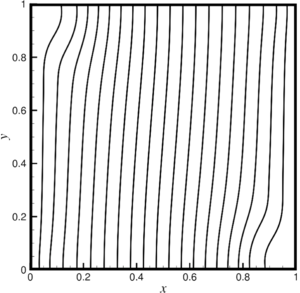
The work is devoted to the peculiarities of free-convective flow of liquids with viscosity temperature anomaly (the presence of extremes on the viscosity curve). Examples of such liquids are polymer solutions, metal melts, well-purified liquid sulfur, and other fluids. The mechanism of the anomalous viscosity behavior of such liquids (in the case of polymers) can be explained by polymerization and depolymerization reactions. At a certain temperature interval, the molecules of a substance interlock, forming long chains and, as a result, increasing the viscosity, then when the upper limit polymerization temperature is reached, the reaction begins that is reverse to the polymerization, which proceeds according to the chain mechanism and results in the sequential cleavage of molecules from the chain and leads to a decrease in viscosity . The features of behavior of such environments are currently not well understood and require increased attention to experimental and theoretical studies, especially now, mainly due to the intensive development of computer technologies and numerical modeling. Based on computational experiments on the process of free convection of a liquid with a Gaussian dependence of viscosity on temperature, the possibility of the existence of isolated regimes of convection of a liquid in a square cell heated from the side is shown. It was assumed that the viscosity function has one extremum and is unambiguously described by two parameters: the ratio of the highest to the lowest viscosity at a given temperature range and the degree of fullness of a given temperature range. As a mathematical model, a system of equations was used in the Oberbeck–Boussinesq approximation. For the numerical solution of the system of equations, the control volume method with the SIMPLE procedure is modified and implemented.
free convection,
heat transfer,
heat and mass transfer,
thermo-viscous fluid,
viscous barrier,
hydrodynamic barrier,
anomalous viscosity
In paper, the features of a free convective flow are numerically investigated liquids with a viscosity temperature anomaly (for example, on the viscosity curve there is an extreme), examples of such liquids can serve as solutions polymers, melts of metals or silicates, well-purified liquid sulfur and other vibes. The mechanism of the anomalous behavior of the viscosity of such liquids, in the case of polymers can be explained by polymerization reactions and depolymerization. On a certain temperature range of the substance molecule attract to form long chains and, as a consequence, the viscosity of such a fluid increasing, then when reaching the upper limit temperature polymerization begins the reverse reaction of polymerization, which also flows through the chain mechanism and consists in the sequential elimination molecules from the chain and leads to a decrease in viscosity. Behavior of such environments are currently not well understood and require increased attention to experimental and theoretical studies, especially in present time, mainly due to the intensive development of computer technology and numerical simulation. Based on the computational experiments of the process of free convection of a fluid with Gaussian dependence viscosity on temperature, it is shown that isolated modes of convection fluid in a square cell, heated from the side. It was believed that the viscosity function has one extreme and uniquely described by two parameters: the ratio of the largest to the smallest value of viscosity at temperature range and degree of fullness temperature range. Also found to be a key factor in the formation of complex structures of convective flows is the parameter FWHM, which is the full width, calculated as the difference between the maximum and minimum values of the argument of the viscosity function, taken on level equal to half its maximum value in the mode of pure thermal conductivity. The system equations in the Oberbeck–Boussinesq approximation were used as a mathematical model. When deriving equations in Oberbeck–Boussinesq approximation is key to the assumption that density deviations from some mean value due to the effects of thermal expansion of a fluid are so small, that they can be neglected in all equations except the momentum equation, where these deviations are significant only in terms of the influence lifting force, which is the cause of convective movements. For the numerical solution of the system of equations modified control volume method implemented with SIMPLE procedure (Semi-Implicit Method for Pressure Linked). Presents the results of computational of experiments of free convective flows and mass transfer of liquid with non-monotone dependence of the viscosity on the temperature of the Gaussian type in square cell with vertical isothermal and horizontal adiabatic boundaries with a constant temperature difference applied to vertical cell borders. It is established that when the value of the parameter FWHM more than a quarter of the considered temperature range, transition from the multi-eddy mode convection with non-linear temperature distribution and “S-shaped” “viscous barrier” to slow global single-vortex convection with linear temperature profile and, accordingly, vertically located “viscous barrier”. At the same time there is a monotonous damping of the maximum component of the velocity vector and the integral heat transfer in the cell, aspiring to the regime of pure thermal conductivity. When FWHM less than a quarter of the temperature range in question occurs the formation of additional vortex structures that with increasing maximum viscosities increase and result in complex multiscale flows. In this case, for sufficiently large values maximum viscosity occurs differentiation flow by the “viscous barrier”, which, in turn, breaks the cell into two isolated subregions, where there is a flow extended vertically near the isothermal walls, the heat flux propagates normally to the “viscous barrier”, which, in turn has a nearly vertical profile. With decreasing FWHM parameter regardless of the maximum viscosity for maximum values of the components of the velocity vector and integral heat transfer in a cell, their monotonous increase is characteristic, with the values asymptotically tend to values characteristic of a fluid with constant viscosity.