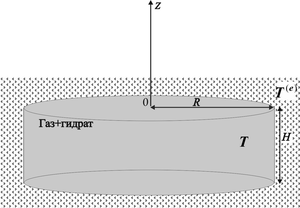
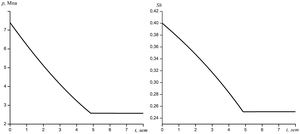
The paper considers a homogeneous reservoir in the form of a pancake with characteristic linear dimensions corresponding to real deposits: with a radius of the order of several kilometers, and a height of tens of meters. Since the radii of such layers are much larger than their thickness, this allows one to take into account the thermal interactions of the field with the surrounding rocks through the upper and lower boundaries of the layer in a flat one-dimensional approximation. To describe the model, such basic equations were used as the law of conservation of mass of gas and water in the reservoir, the equation of heat balance and temperature fields near the reservoir boundary, as well as initial and boundary conditions. The constructed theoretical model makes it possible to analyze the possibility of realizing the complete gas recovery of the layers only due to the thermal reserve of the hydration layers themselves, as well as the surrounding mountain massif. For the values of the parameters that determine the initial state of the board, numerical experiments were performed. The dynamics of reservoir pressure and hydrate saturation in the reservoir are presented. As a result of the research, it was established that at a constant gas extraction rate, the achievement of reservoir pressure up to 2.6 MPa and, accordingly, a temperature of 273 K occurred in about 5 years. It is shown that when gas is taken from a reservoir with a radius of 3000 m and a thickness of 50 m, its hydrate saturation decreases by about 38% over 5 years.
gas hydrate,
porous medium,
phase transition
Purpose: Numerical study of gas extraction from a gas hydrate reservoir without exposure to external sources.
The paper considers a homogeneous reservoir in the form of a pancake with characteristic linear dimensions corresponding to real deposits: with a radius of the order of several kilometers, and a height of tens of meters. Since the radii of such layers are much larger than their thickness, this allows one to take into account the thermal interactions of the field with the surrounding rocks through the upper and lower boundaries of the layer in a flat one-dimensional approximation.
Methods: A finite-difference scheme based on the use of the Euler method was chosen as a numerical method for solving a system of partial differential equations.
Results: The following parameters characterizing the state of the gas hydrate reservoir were used in this task: a radius of
Conclusion: as a result of the study, it was established that at the given parameters for a gas hydrate reservoir, the achievement of reservoir pressure up to 2.6 MPa and, accordingly, a temperature of 273 K occurred in about 5 years. It is shown that when gas is taken from a reservoir with a radius of 3000 m and a thickness of 50 m, its hydrate saturation decreases by about 38% over 5 years.